Fraction Models
The three major categories of fraction models are the area model, linear model, and set model. Evidence suggests that providing opportunities for students to work with all three models plays a crucial role in developing a conceptual understanding of fractions. Having students repeat an activity with a different model and asking them to make connections between models can also be useful. Too often, students learn rules for manipulating written fractions before they have developed an understanding of fraction concepts. Using fraction models can help students clarify ideas that are often confused in a purely symbolic mode and construct mental referents that enable them to perform fraction tasks meaningfully.
THREE CATEGORIES OF FRACTION MODELS
1. AREA MODEL: In the area model fractions are represented as parts of an area or region. Useful manipulatives include rectangular, or circular fraction sets, pattern blocks, geoboards and tangrams.
Rectangular, or circular fraction sets can be used to develop the understanding that fractions are parts of a whole, to compare fractions, to generate equivalent fractions and to explore operations with fractions. While the rectangular model is easier for students to draw precisely, the circular model emphasizes the part-whole concept of fractions and the meaning of the relative size of a part to the whole (Cramer, Wyberg & Leavitt, 2008). Hence, students should have opportunities to work with both rectangular and circular models.
When purchasing rectangular or circular fraction sets keep in mind that those with pieces that are not labeled provide more opportunities for learning. Labeled kits deprive students of opportunities to think about the size of the pieces in relation to the whole and also lead students to incorrectly assume that only one of the pieces can be considered as the whole, thereby making them less useful when working on concept of unit activities in which students name fractions when the unit is varied.
Sample Activities:
Make One Whole (ver. 1)
Equivalent Fractions Exploration (ver. 1)
Adding Like Fractions
Subtracting Like Fractions
Pattern blocks allow students to see how shapes can be partitioned into other shapes. Consisting of blocks in six geometric shapes they are referred to as green triangles, orange squares, blue parallelograms, tan rhombuses, red trapezoids, and yellow hexagons. When students work only with the yellow, red, blue, and green blocks, and the yellow block is given the value of 1, a red block represents one-half, a blue block represents one-third, and a green block represents one-sixth.
Sample Activities:
Pattern Block Fractions
Quadrilateral Fractions
What Fraction is Red?



Geoboards can be used to explore
a range of math concepts including properties of shapes, area, and
perimeter. Available in a variety of
sizes they also provide an engaging way for students to partition wholes into equal
areas and to explore equivalent fractions using an area model.
Sample Activities:
Partition a Square (ver. 1)
Partition a Square (ver. 3)
The standard tangram consists of seven shapes that can be arranged to form a square. Frequently used for exploring geometry, they can also be used for problem solving tasks involving fractions.
Sample Activity:
The Warlord's Puzzle
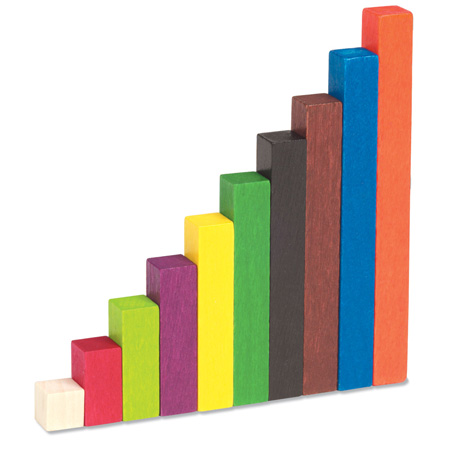
2. LINEAR MODEL: In the linear model lengths are compared instead of areas (e.g., 3/4 of an inch). Either number lines are drawn and subdivided or physical materials are compared on the basis of length. Useful manipulatives include Cuisenaire rods or fraction strips that are easily connected to ideas about fractions on a number line.
Cuisenaire Rods are rectangular rods,
each of a different color and size, that can be used to help students develop
understanding of a range of math concepts including addition, subtraction, multiplication, length, area, volume, and fractions. The lengths of the different colored rods
increase incrementally from the smallest size (1cm long) to the largest size
(10 cm long). The rods are flexible because any length can be used to represent the whole. For example, in order to work with 1/4 and 1/8 students would use the brown rod which is 8 units long. The purple rod would then become 1/2, the red rod would become 1/4, and the white rod would become 1/8.
Sample Activities:
Cuisenaire Fractions
Representing Unit Fractions
Match the Length
Mixed Number x Fraction Models
Divide a Whole Number by a Unit Fraction (ver. 2)
The number line is an important linear model for students to work with as it reinforces the fact that there is always one more fraction to be found between two fractions.
Sample Activities:
Fractions on a Number Line
Roll a Fraction
Fraction Strips can be used to explore equivalency, comparison of fractions, ordering fractions and number operations with fractions. If purchasing commercially made strips opt for those that are unlabeled to provide more opportunities for thinking and learning.
Sample Activities:
Making Fraction Strips (ver. 1)
Equivalent Fractions Exploration (ver. 2)
3. SET MODEL: In the set model the whole is understood to be a set of objects, and subsets of the whole make up fractional parts (e.g. ½ of the class, ¼ of a set of buttons, 1/3 of a tray of muffins). Useful manipulatives include two-color counters, centimeter cubes, or any set of objects that can be counted (e.g. a bag of marbles).
Typically red on one side and yellow on the other two color counters can be flipped to change their color and model various fractional parts of a set.
Sample Activities:
Fractional Parts of a Set
Equivalent Fractions: Set Model
OTHER USEFUL MANIPULATIVES
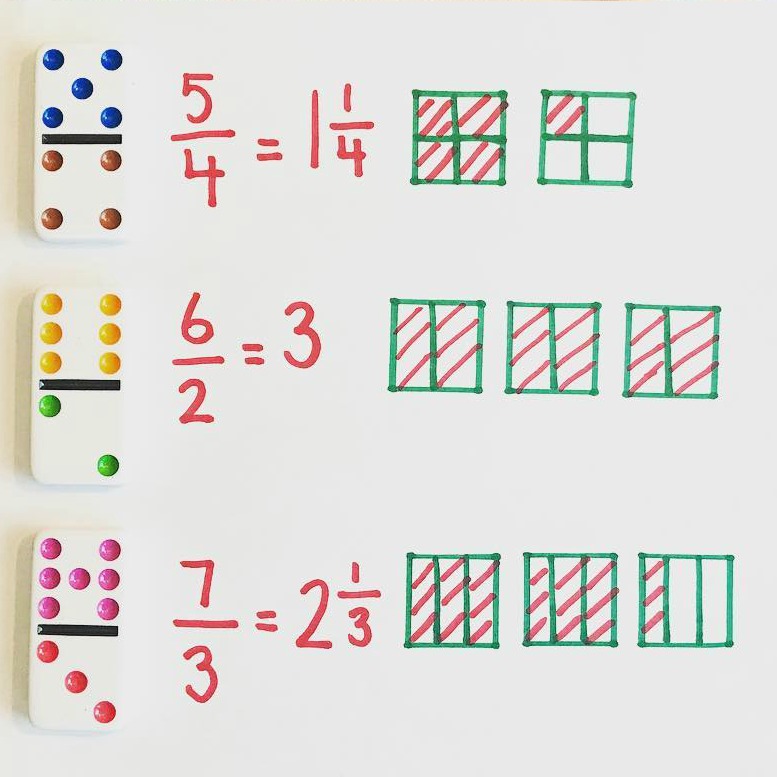
Other useful manipulatives that can be used in math centers to develop fraction concepts and skills include dominoes, fraction cards and fraction dice. When purchasing dominoes look for a Double Nine set (55 dominoes) so that you have a range of fractions greater than one .
Sample Activities:
Equivalent Fractions: Dominoes
Renaming Fractions Greater Than One