Place Value Strategies

What are place value strategies and how do they relate to standard algorithms? The Common Core State Standards describe the requirements for fluent use of the standard algorithms for addition, subtraction, multiplication and division as follows:

4.NBT.4 Fluently add and subtract multi-digit whole numbers using the standard algorithm.
5.NBT.5 Fluently multiply multi-digit whole numbers using the standard algorithm.
6.NS.2 Fluently divide multi-digit numbers using the standard algorithm.
6.NS.3 Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.

Prior to developing fluency with standard algorithms the CCSS emphasize place value strategies. This strong focus on place value strategies plays a critical role in the development of mental and written computation strategies, while providing students with the opportunity to develop a deep understanding of how the standard algorithms work. Common Core Standards explicitly referencing strategies based on place value include 1.NBT4, 2.NBT.5, 2.NBT.6,  2.NBT.7, 3.NBT.2, 3.NBT.3, 4.NBT.5, 4.NBT.6, 5.NBT.6, and 5.NBT.7.

So, what do place value strategies look like? Many different strategies based on place value exist for both written and mental computations. A few examples of written methods for Grades 2-5 are shown below.

Possible 2nd Grade Place Value Strategies

Addition on an open number line.

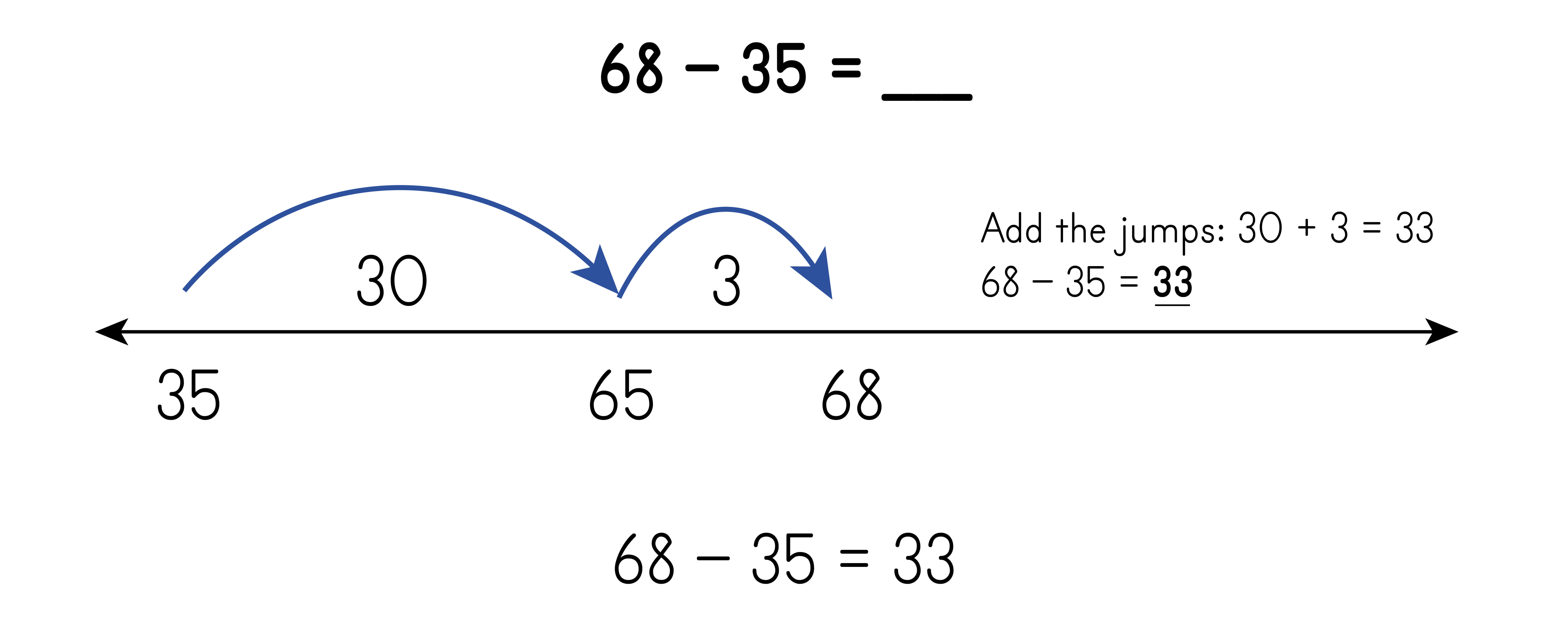
Subtraction on an open number line. Adding up from the subtrahend to the minuend.

Addition using Expanded Form: Each addend is represented using expanded notation. Like place values are added.

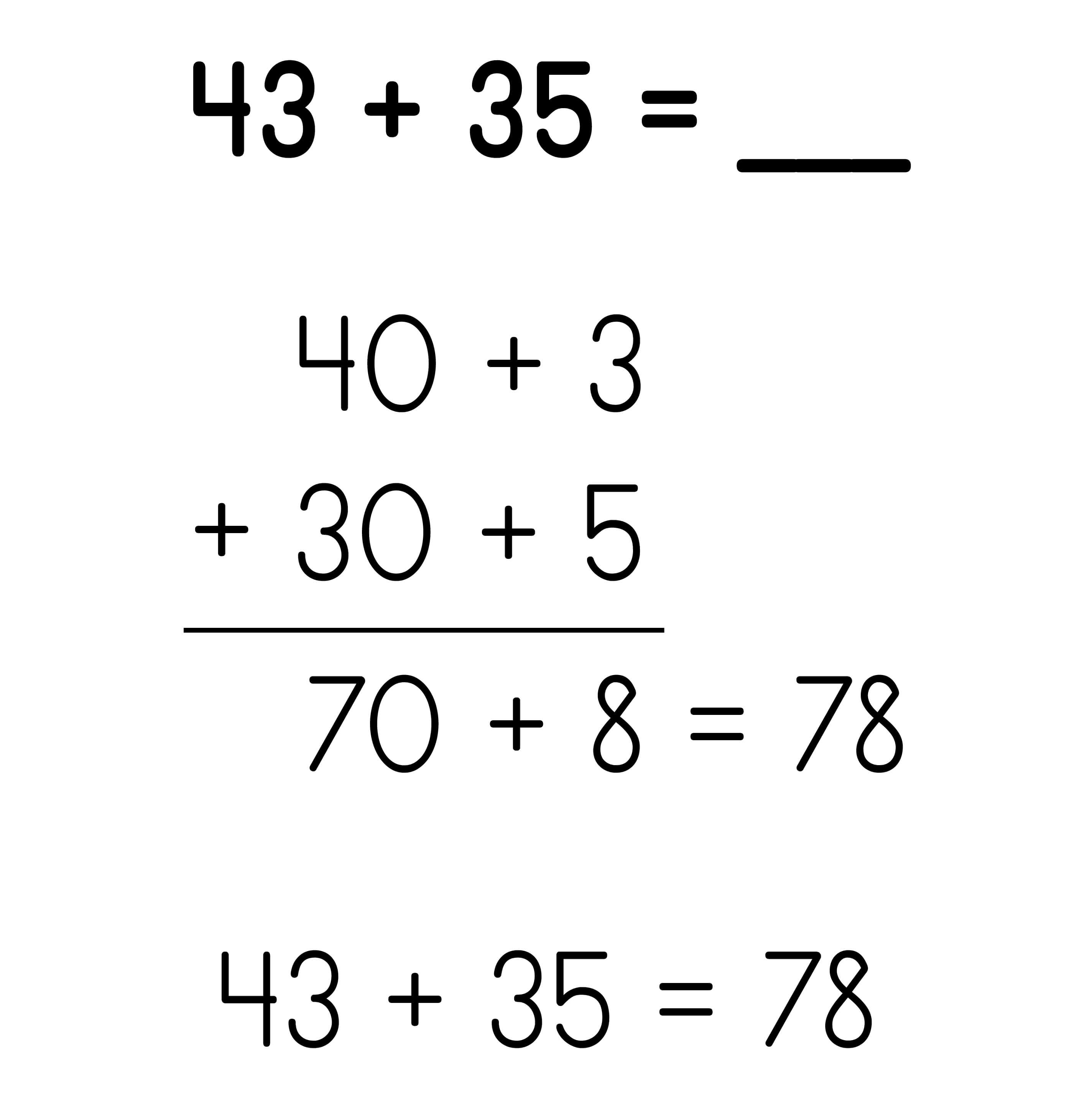
Subtraction using Expanded Form: The minuend and subtrahend are represented using expanded notation. Like place values are subtracted.

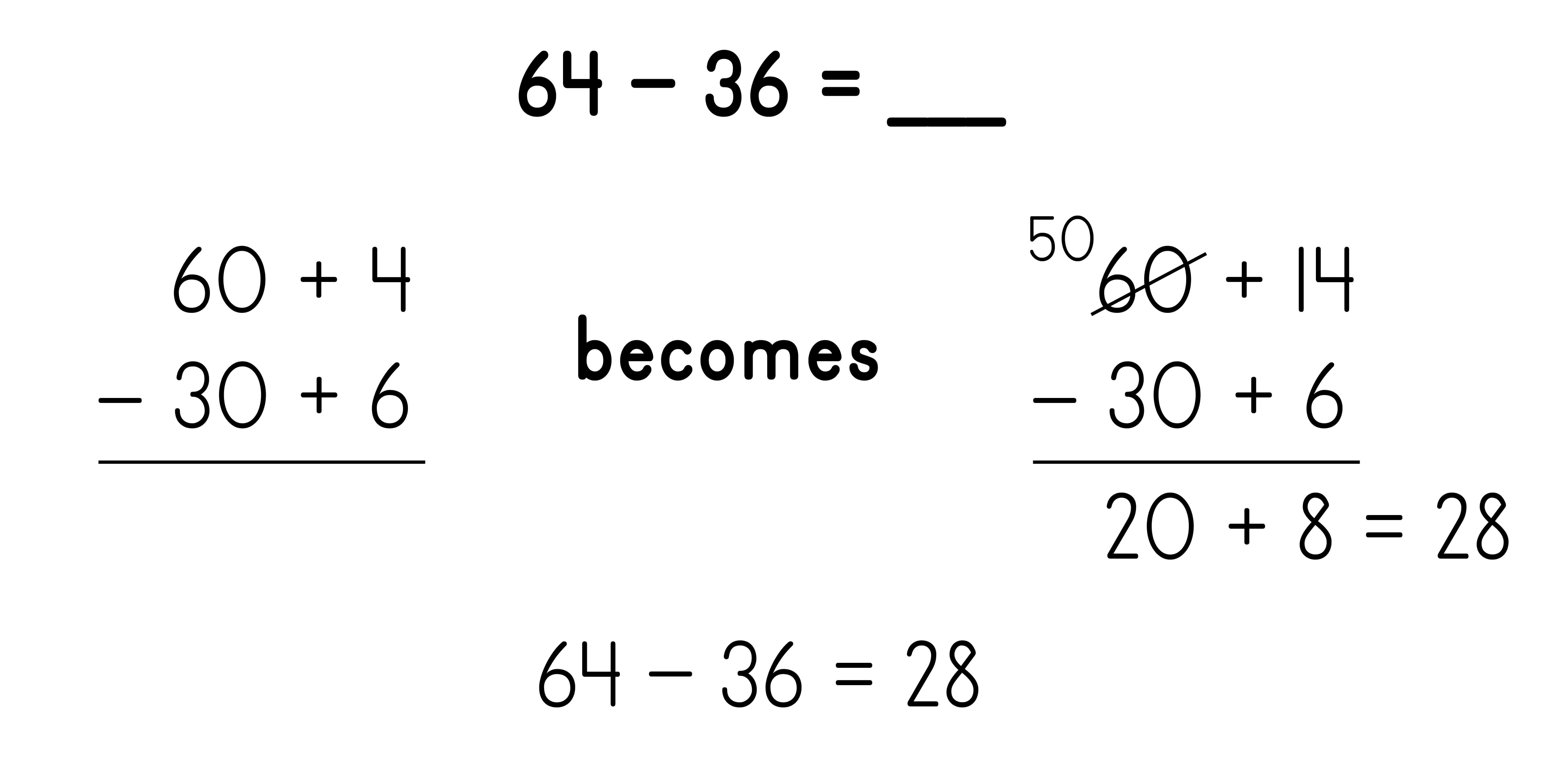
Possible 3rd Grade Place Value Strategies

Partial Sums Addition

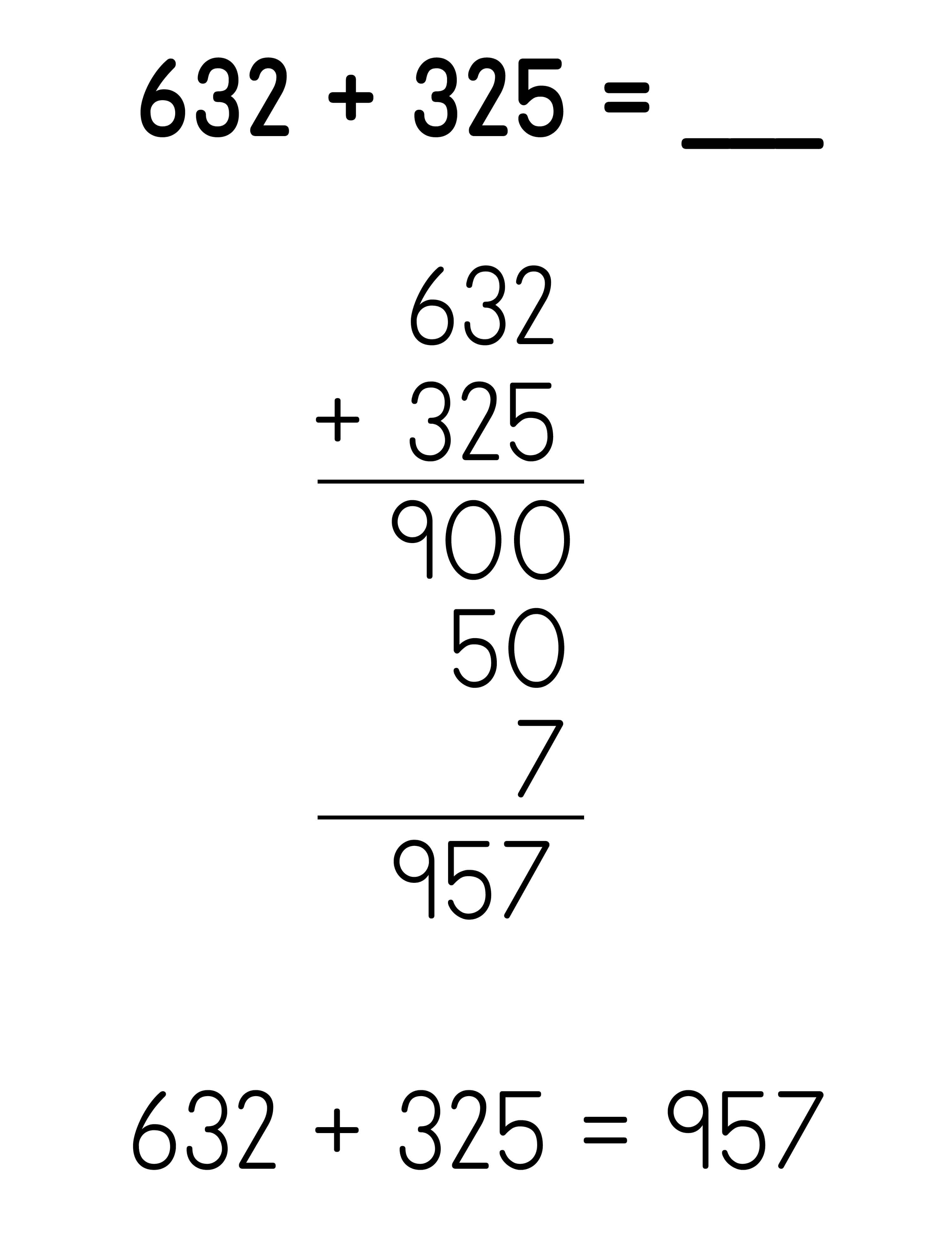
Use place value to multiply  1-digit x a multiple of ten

9 x 80 = ?

9 x 80 = 9 x 8 tens
           = 72 tens = 720
9 x 80 = 720

Use the distributive property to multiply within 100

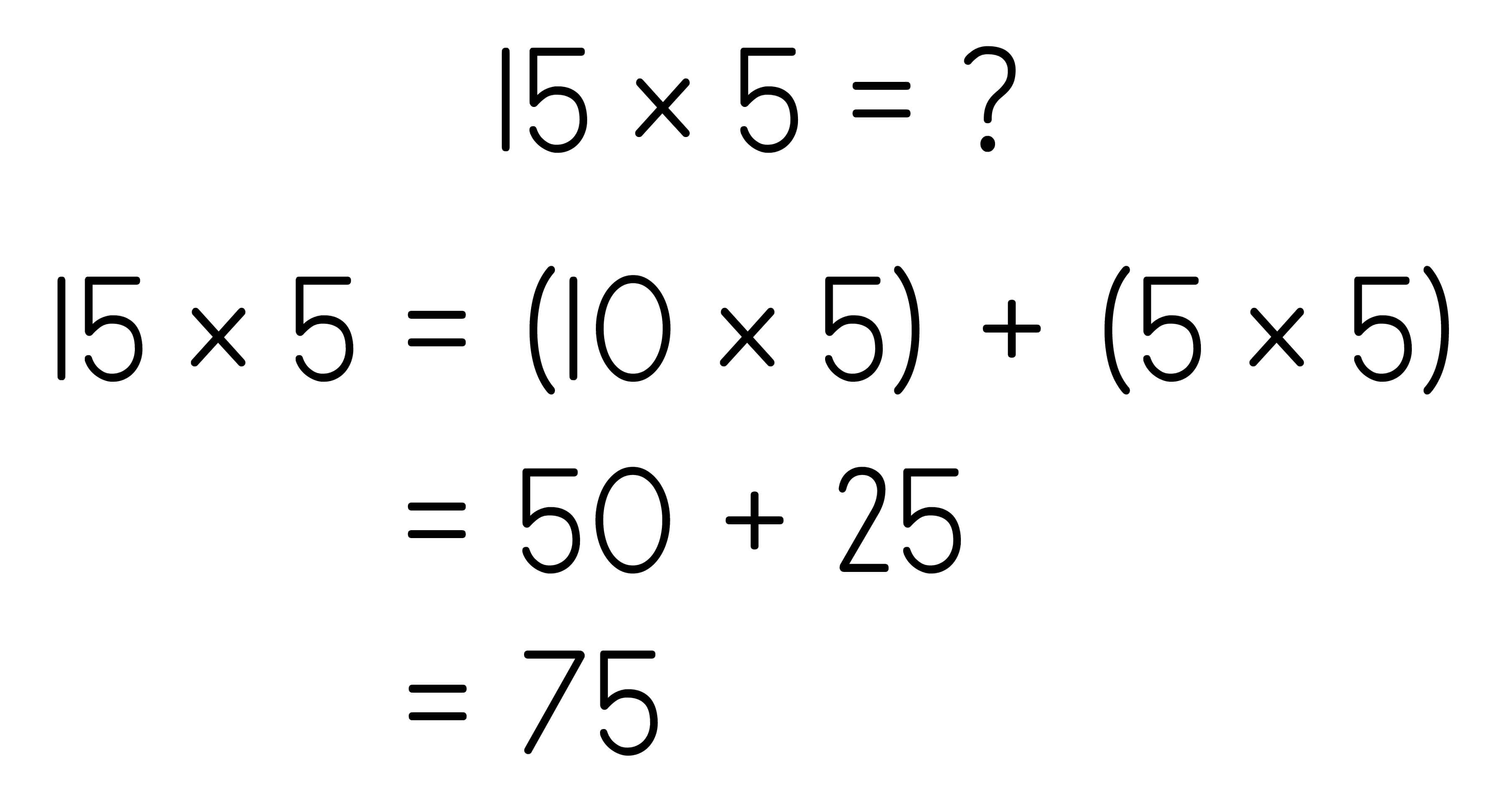
Possible 4th Grade Place Value Strategies

Area Model: 1 x 3-digit

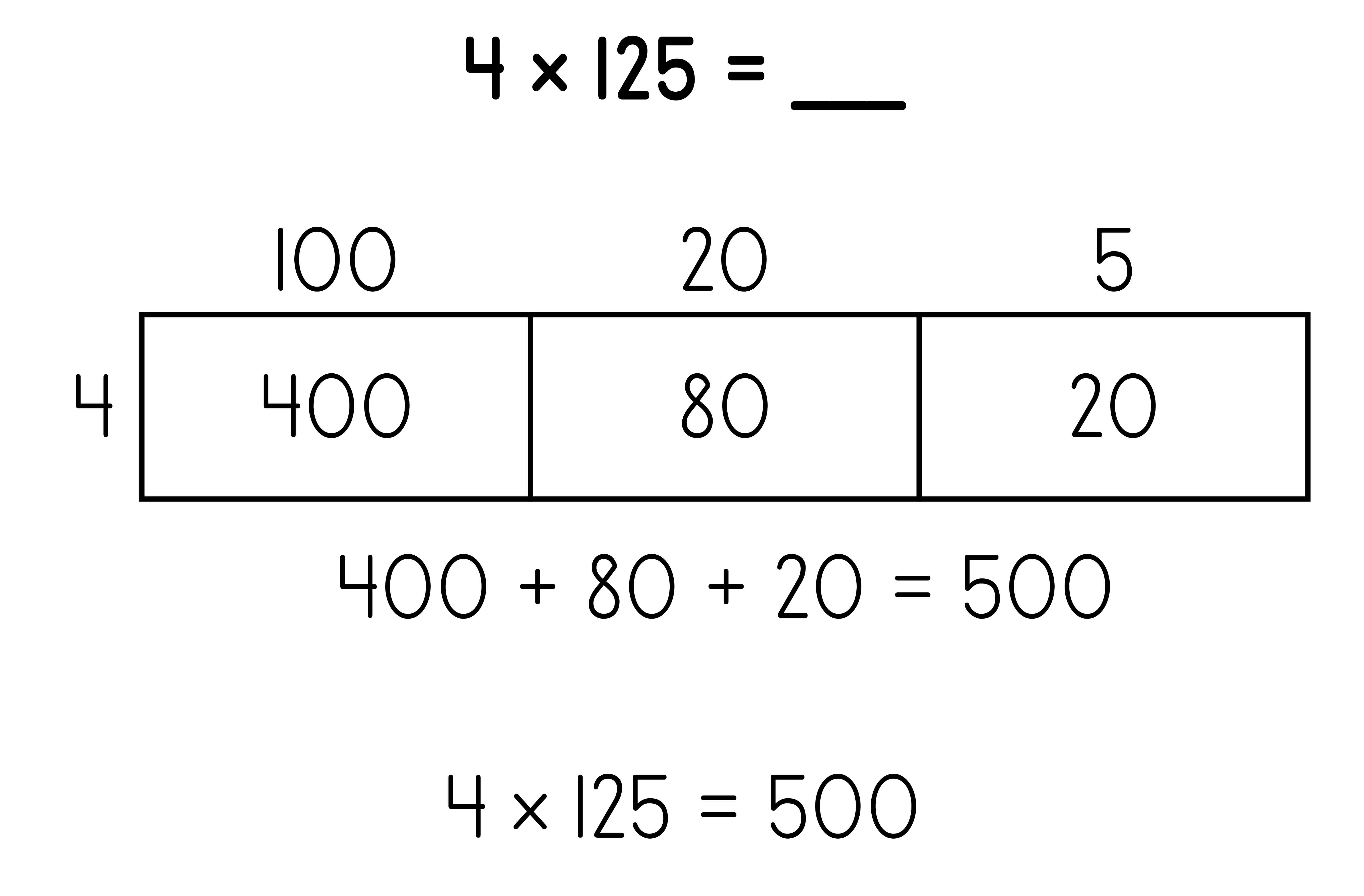
Area Model: 1 x 4-digit

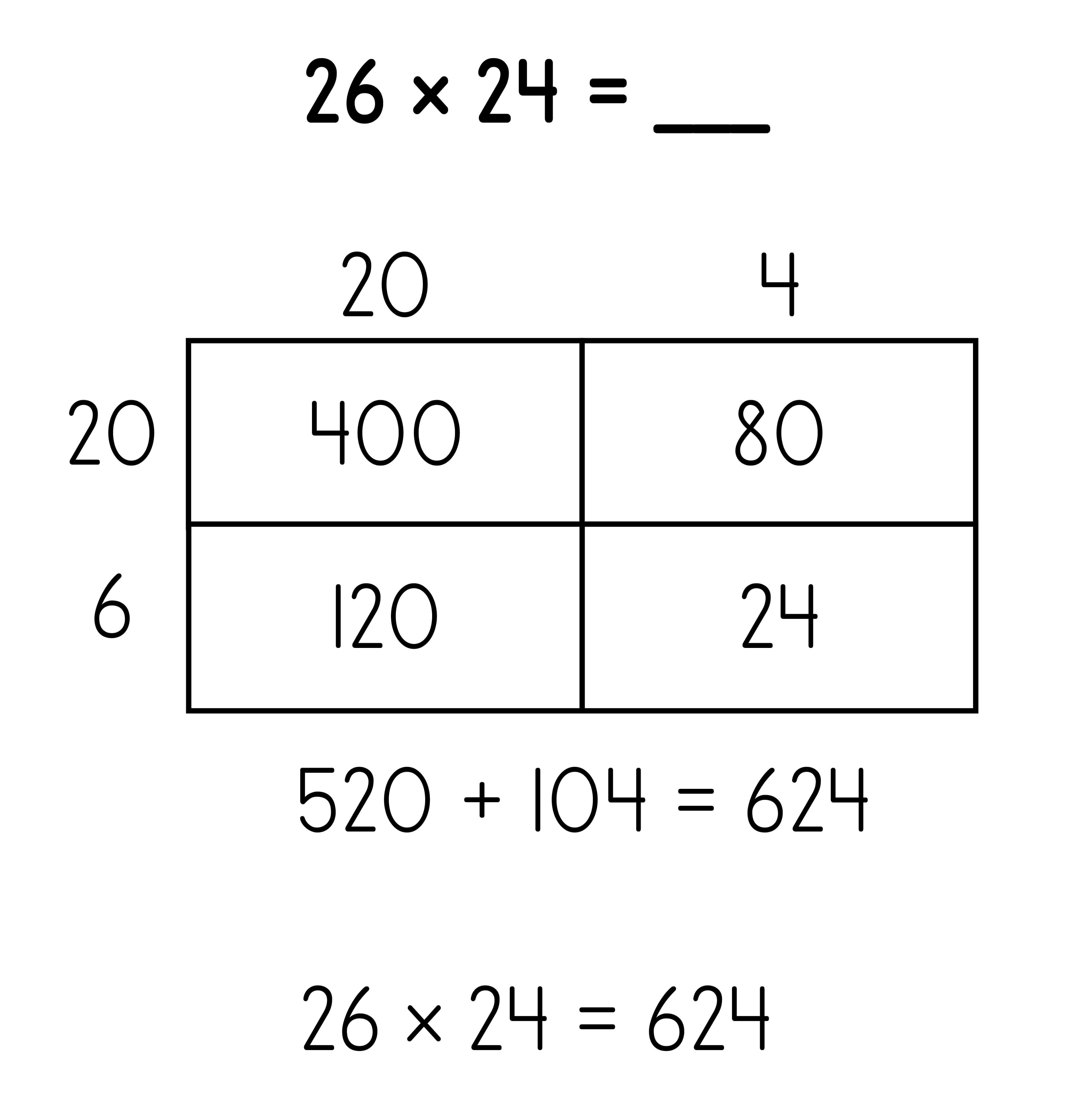
Area Model: 2 x 2-digit

Partial Products: 2 x 1-digit

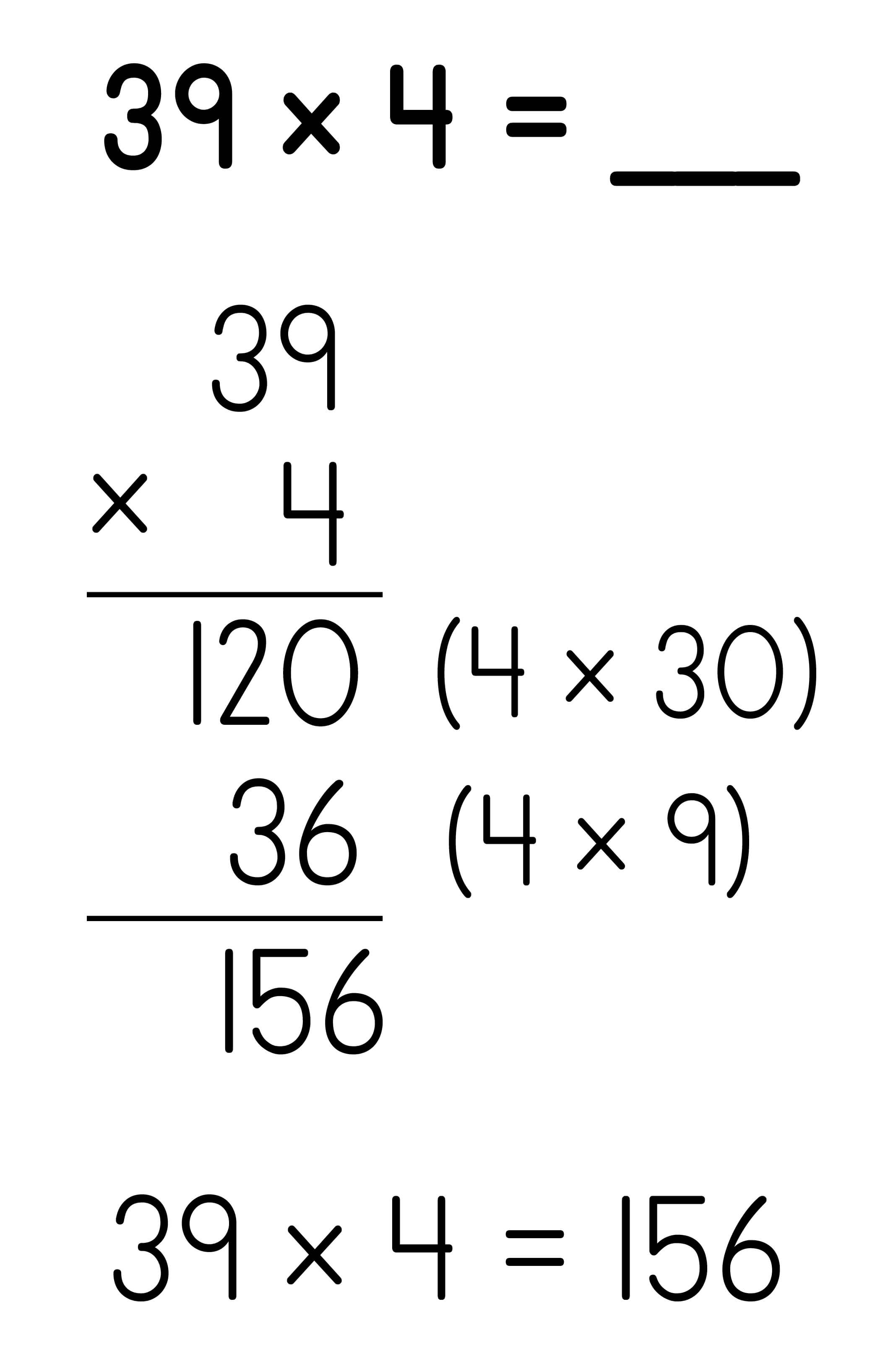
Partial Products: 3 x 1-digit

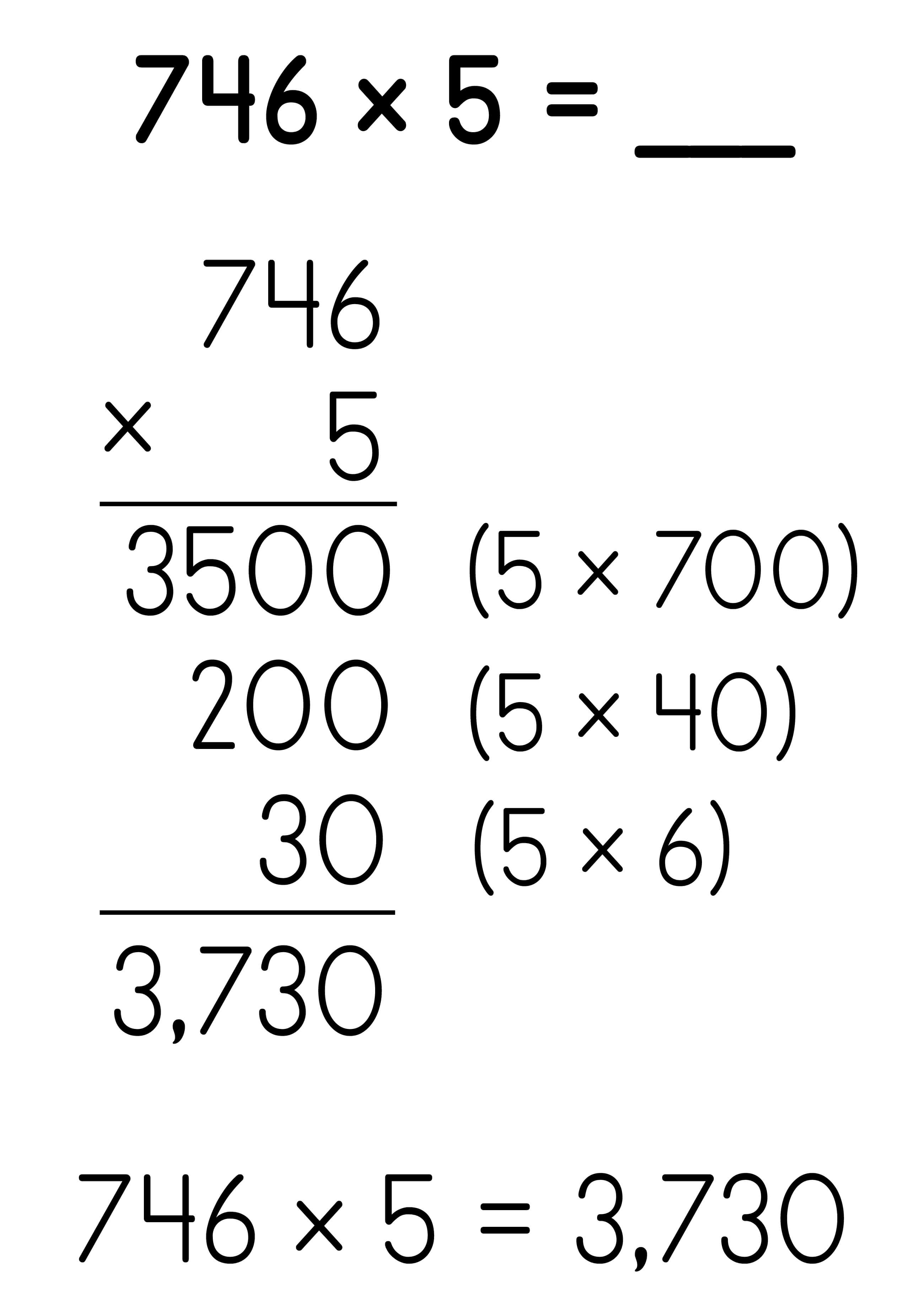
Partial Products: 2 x 2-digit

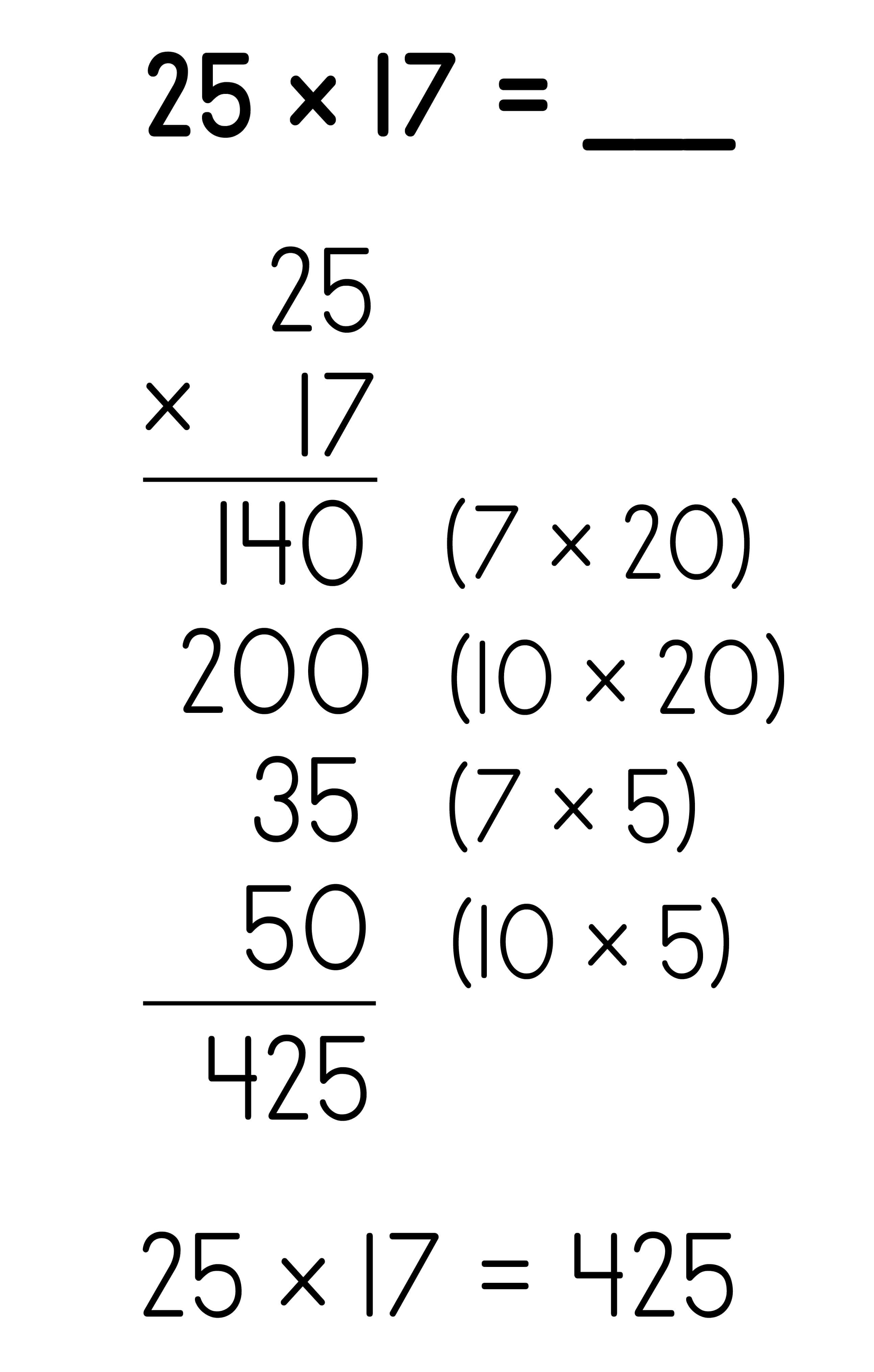
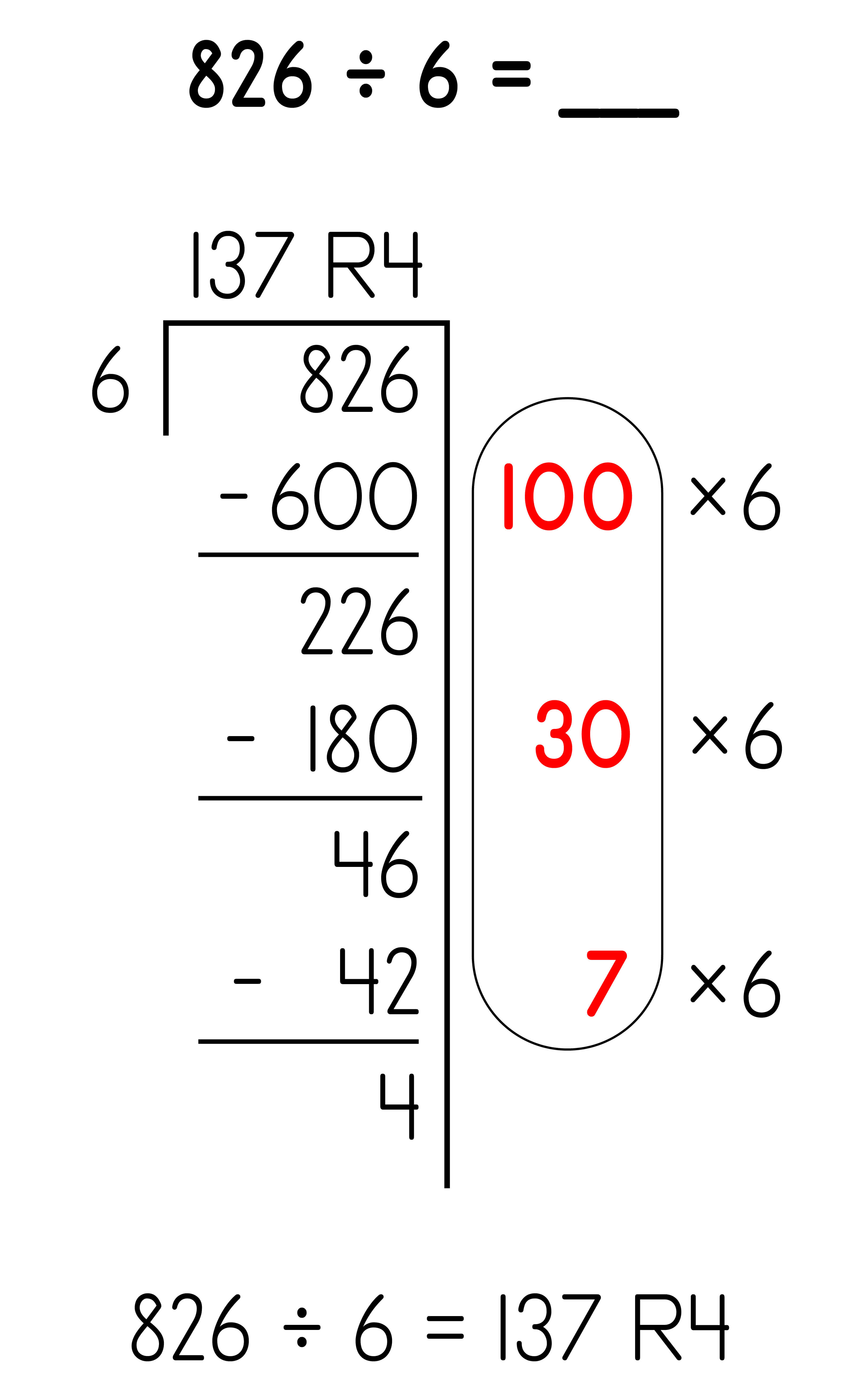
Partial Quotients: 3-digit dividend

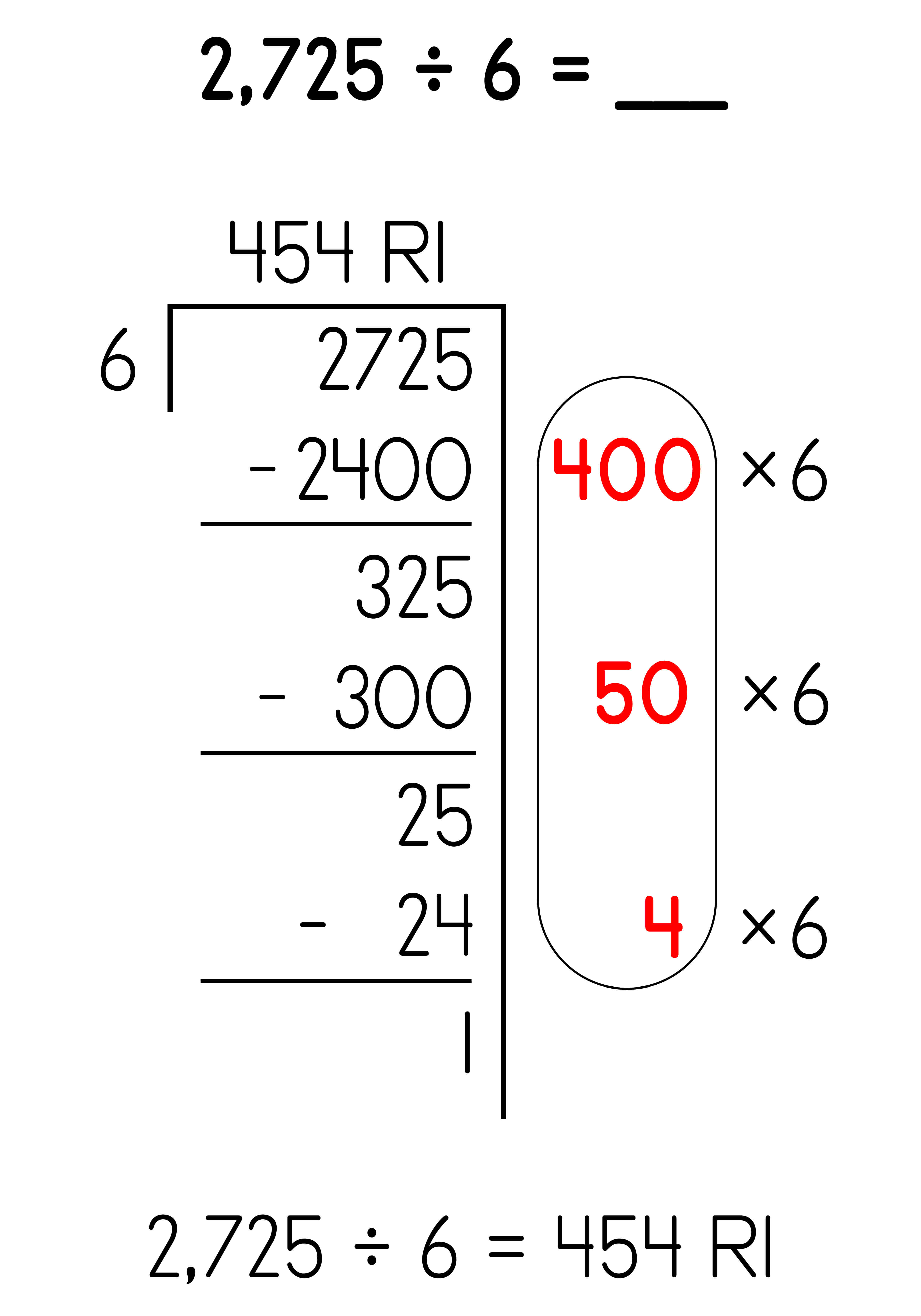
Partial Quotients: 4-digit dividend

Multiply Up for Division: 3-digit dividend

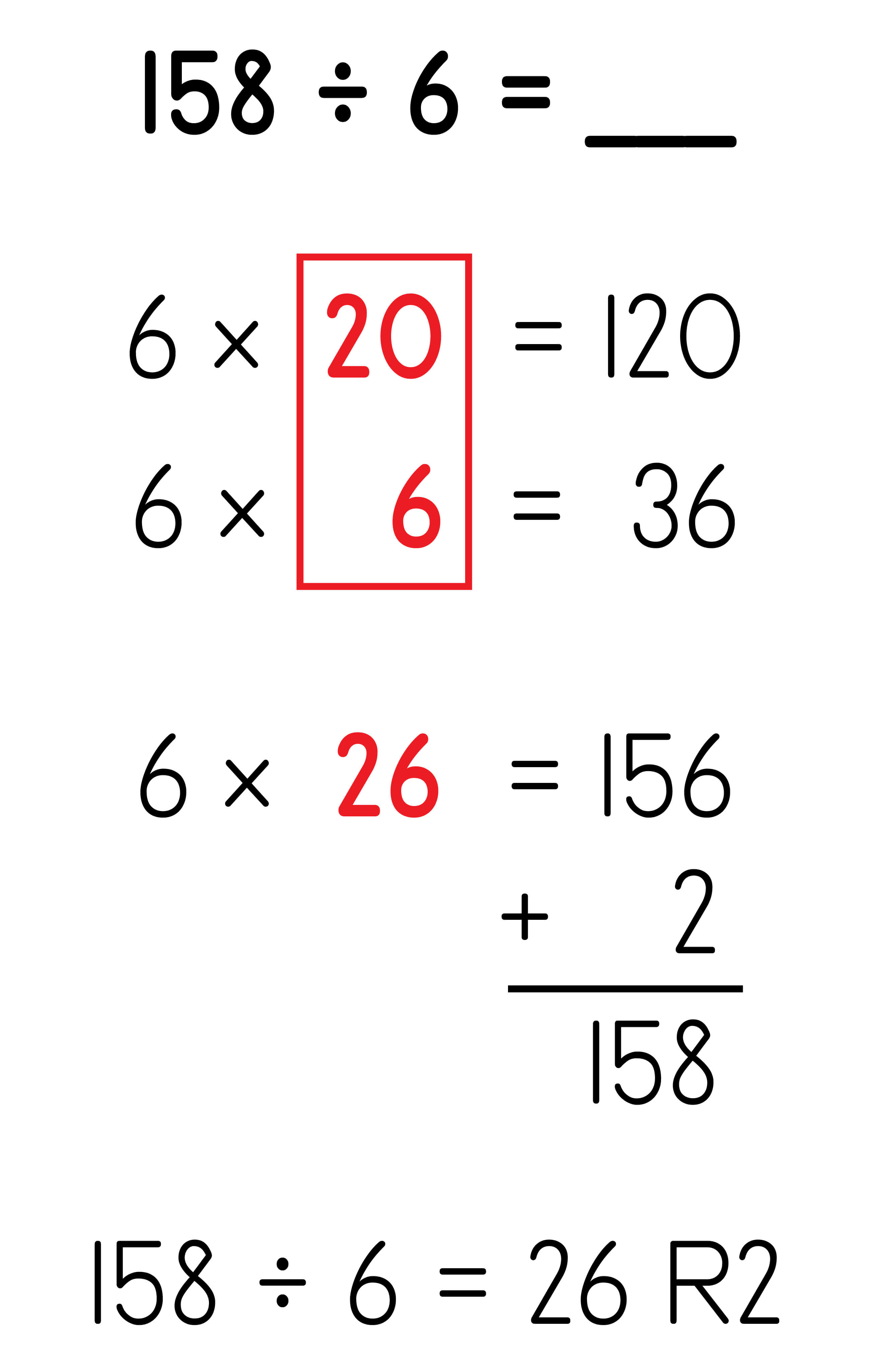
Multiply Up for Division: 4-digit dividend

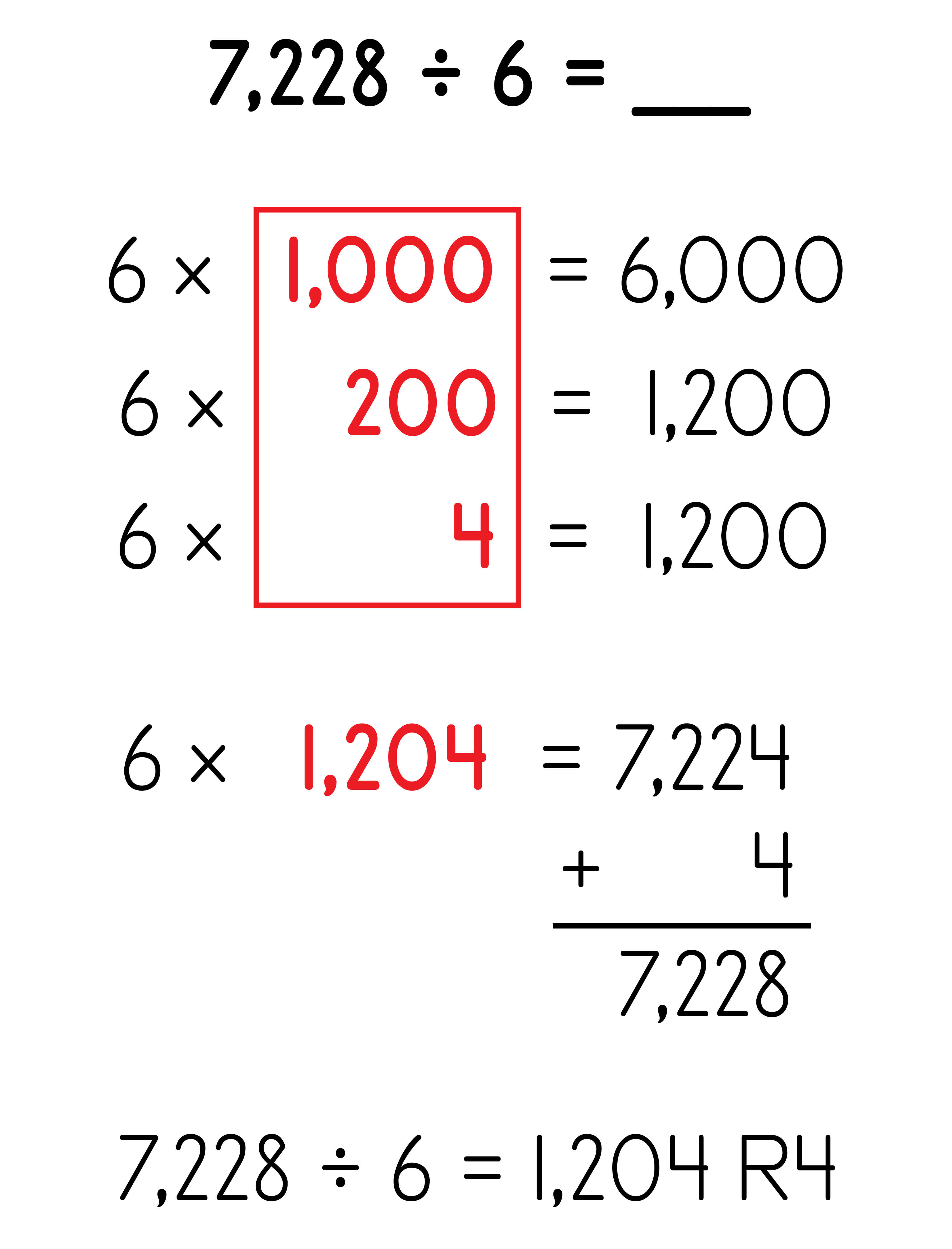
Possible 5th Grade Place Value Strategies

Area Model: Multiply decimals using base ten blocks

Multiplying decimals with base 10 blocks

Divide decimals by drawing base ten blocks

Dividing decimals with base 10 blocks

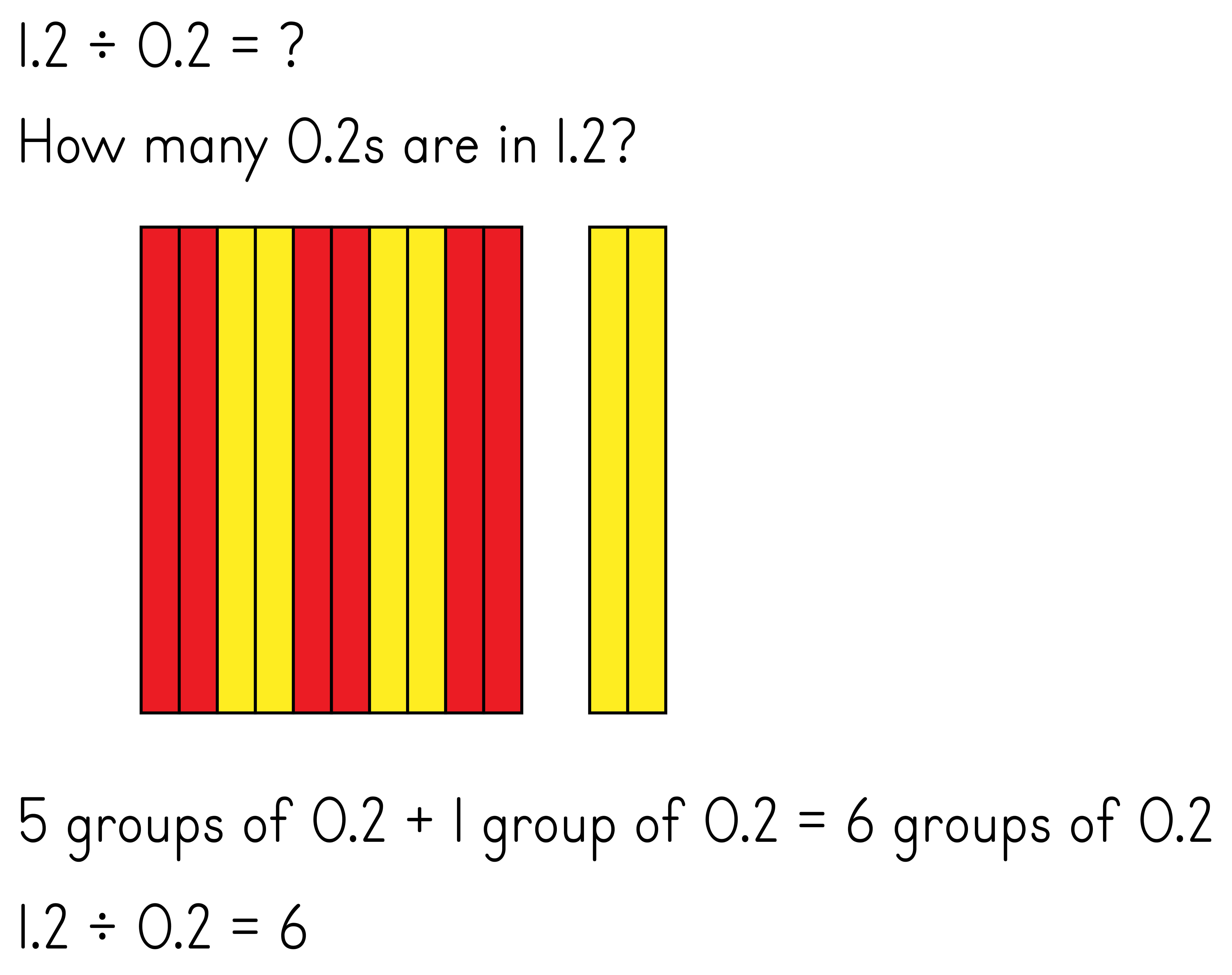
Regardless of which place value strategies are taught it is important that there is consistency across each grade level, and that a clear progression is maintained from one grade level to the next within a school. Time needs to be allocated to school wide discussions to ensure that place value strategies are being used or adopted. The following questions can be used to promote discussion and the selection of 1-2 focus strategies per grade for each operation:

  • Which written methods for addition, subtraction, multiplication and division do we currently teach as a school?

  • Do we have enough emphasis on place value strategies throughout the school? 

  • Are there written methods we don’t use at the moment?  Do we need to adopt them?
  • What mental calculation skills are needed in order for students to use written methods based on place value? Do our students have the necessary mental calculations skills needed?

  • How can we develop whole school agreement on the written methods that we will teach for addition, subtraction, multiplication and division? How will consistency and progression be maintained?