What is an Empty Number Line?
The empty number line, or open number line as it is sometimes referred to, was originally proposed as a model for addition
and subtraction by researchers from the Netherlands in the 1980s. A
number line with no numbers or markers, essentially the empty number
line is a visual representation for recording and sharing students’
thinking strategies during the process of mental computation.
Before using an empty number line students need to show a secure
understanding of numbers to 100. Prior experiences counting on and back
using number lines, recall of addition and subtraction facts for all
numbers to ten and the ability to add/subtract a multiple of ten to or
from any two-digit number are all important prerequisite skills.
Introducing the Empty Number Line
During this stage students practice moving to given numbers in the least number of jumps. Possible questions may include:
Students should be encouraged to share different strategies and discuss
which strategy is the most efficient. For example, when jumping from 0
to 59 one student could make five jumps of ten and nine jumps of one,
while another may make 6 jumps of ten to 60 and then jump back one to
59.
Using the Empty Number Line to Solve Addition and Subtraction Problems
During the next phase students solve addition and subtraction problems
and draw the jumps to explain their thinking process. Students are free
to choose what type of jumps they will use. Again the focus is on
sharing different strategies in order to lead students to use the empty
number line efficiently when adding or subtracting numbers. Possible questions might include:
- How can we go from 27 to 53 in a small number of jumps?
Who has another way? - How can we go from 62 to 45 in a small number of jumps?
Who has another way? - How can we solve 34 + 23 on an open number line?
- How can we solve 37 + 25 on an open number line?
- How can we solve 47 - 23 on an open number line?
- How can we solve 82 - 47 on an open number line?
- How can we solve 56 + ? = 77 on an open number line?
- How can we solve ? - 50 = 20 on an open number line?
- How can we solve ? - 43 = 31 on an open number line?
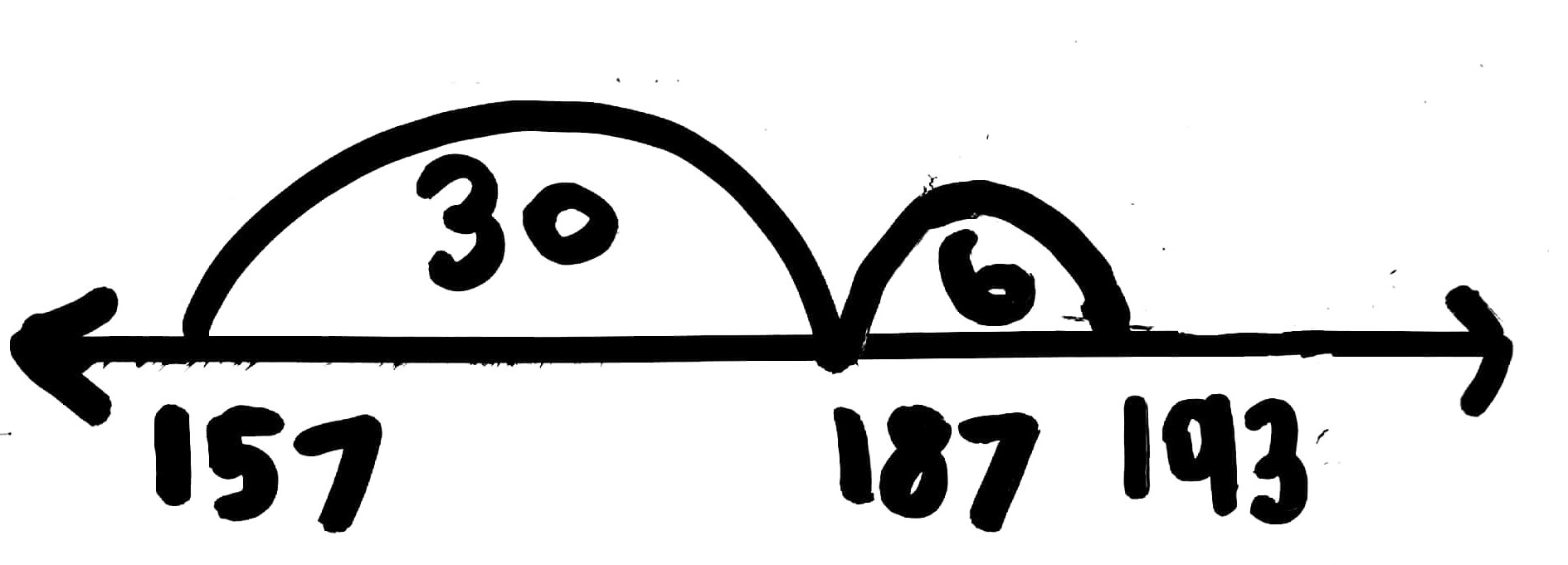
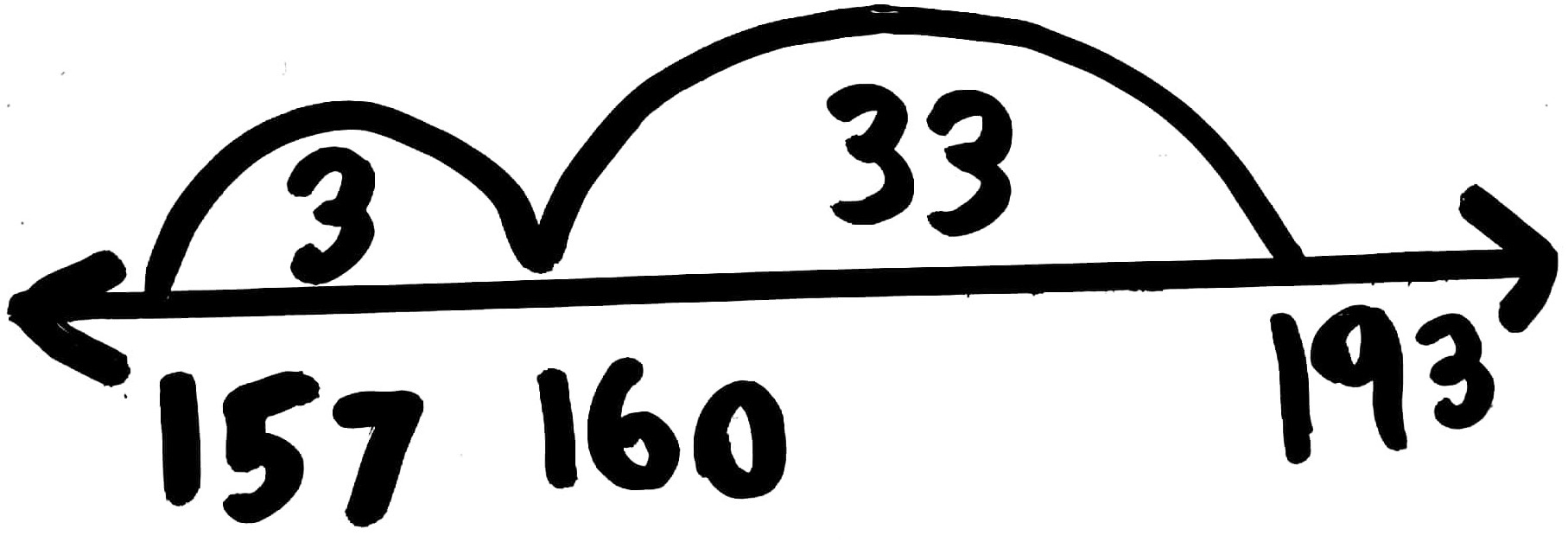
One of the interesting things about mental calculations is that we do not all think the same way. The empty number line allows students to see the variety of ways that the same question can be solved. For example, to solve 157 + 36 a student may begin at 157 and add 30, then 6 or start at 157 and add 3 to get to the next multiple of ten (160) and then add 33. Writing equations horizontally forces students to look at the numerals, whereas written vertically students tend to immediately turn to the procedural algorithm.
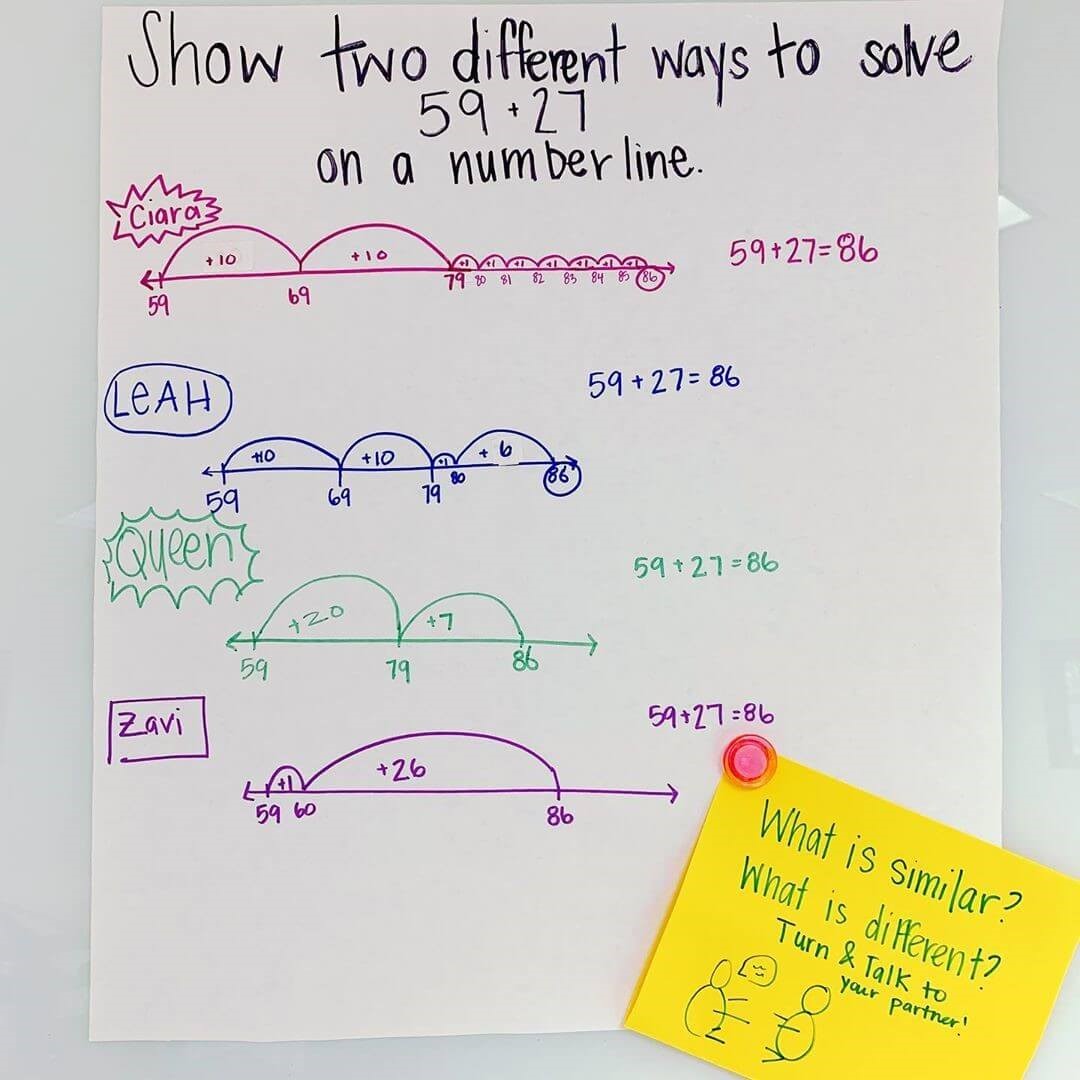
In this 3rd grade classroom, the teacher chose a 2nd grade journal task to review number line strategies for the first math journal task of the year. After working on the task students met for a whole class share to discuss their answer and strategies. The teacher purposely selected four student work samples to highlight different strategies, as well as to set up talk structures that would be used throughout the year.
Using the Empty Number Line to Solve Word Problems
Once students are confident with using the number line for showing their
thinking strategy they can use it to support them while solving a range
of problems in different contexts (e.g. elapsed time, money,
measurement).
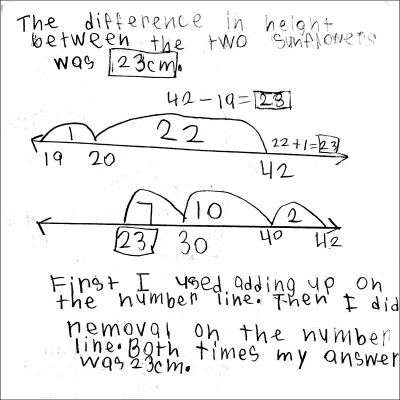
I measured the height of two sunflowers and found that one was 42cm tall and the other was 19cm tall. What was the difference in height of the two sunflowers?
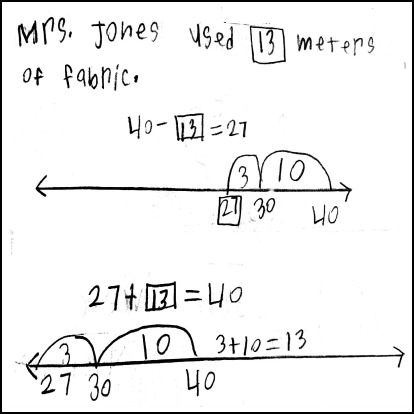
Mrs. Jones had 40 meters of fabric. She used some and had 27 meters of fabric left. How many meters of fabric did Mrs. Jones use?
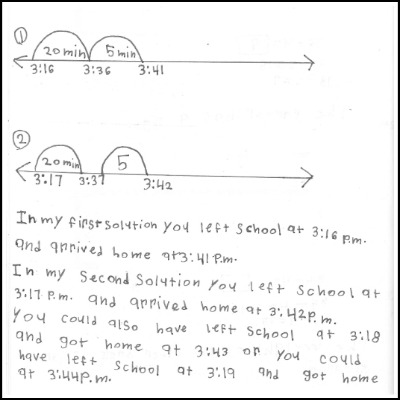
I left school after 3.15 p.m., walked for 25 minutes and was home before 3.45 p.m. What time might I have a) left school b) arrived home? Show two possible solutions.
Addition (3 digit + 3 digit)
On Monday 234 tickets were sold for the school concert. By the time the concert began on Wednesday evening 549 more tickets had been sold. How many tickets were sold in all?
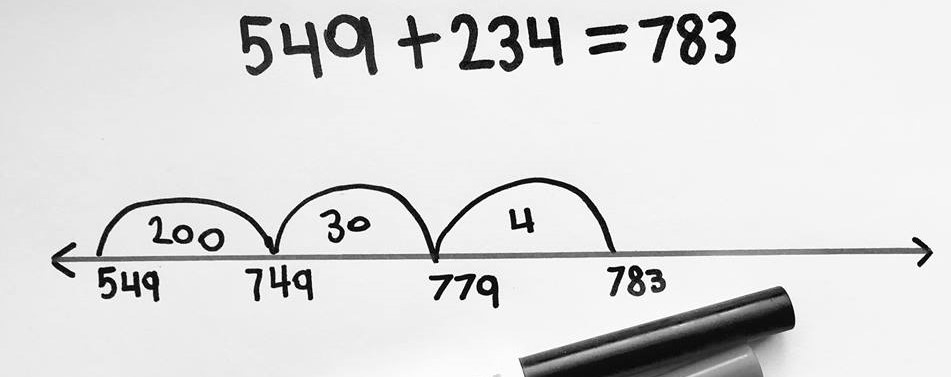
This student started with the larger addend (549) and used place value to decompose the smaller addend into hundreds, tens and ones to make three jumps. Another student in the same class started at 549 and made two jumps of 100, three jumps of 10 and four jumps of 1.
Subtraction (3 digit – 3 digit)
There are 723 people on the subway platform. 239 board a train. How many people are left on the platform?
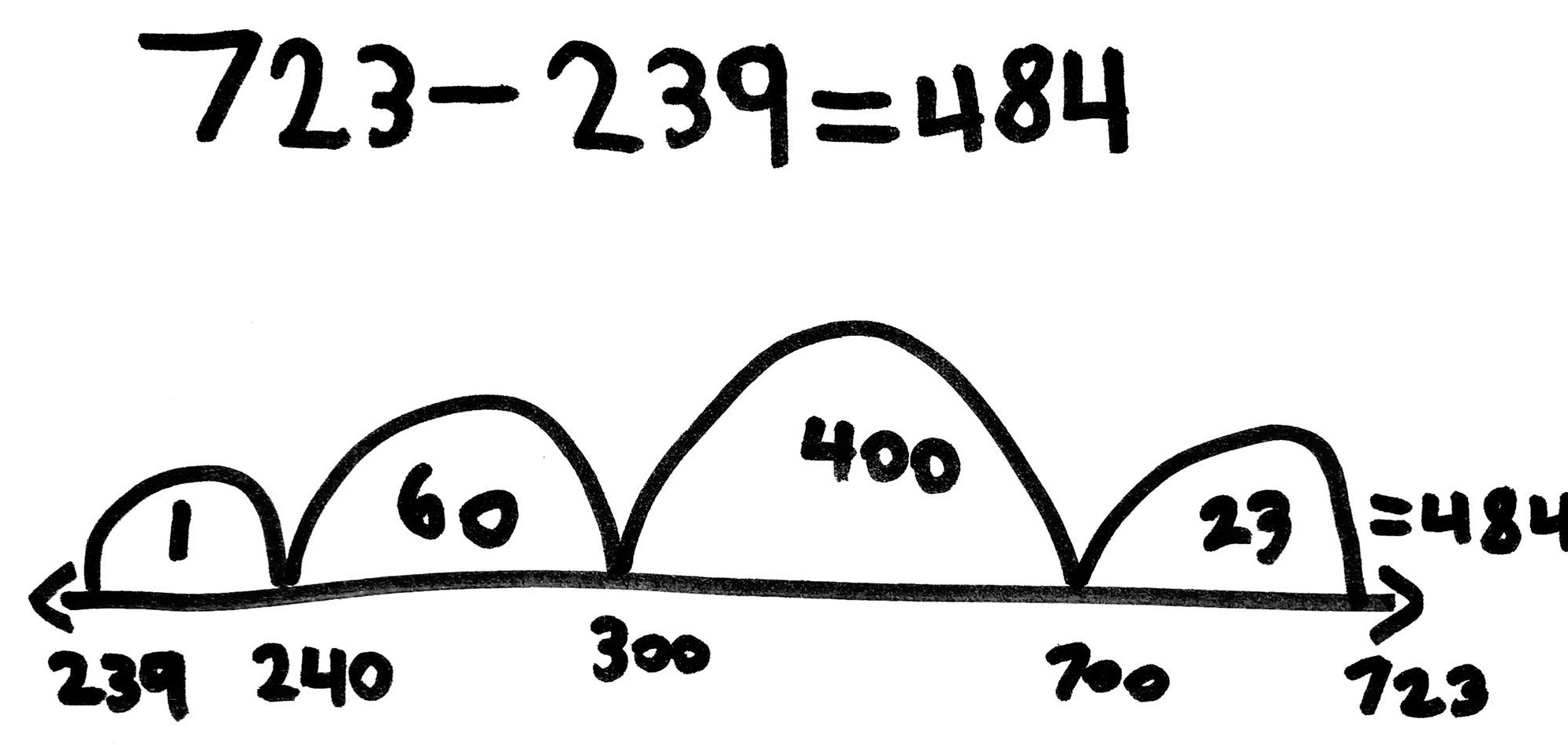
This student started at 239 and added up in 'friendly' jumps to reach 723. Starting with a jump of 1 to reach 240 (multiples of ten and hundred are easy numbers to jump to and from), she then jumped 60 to reach 300, then made a jump of 400 to reach 700 and finally a jump of 23 to reach the minuend 723. She then mentally added her jumps (400 + 60 + 23 + 1) to find the difference of 484.
Multiplication:
Example: Use an empty number line to calculate 19 x 4
20 (a ‘friendly’ number) is one more than 19. We can do 4 jumps of 20 to 80 and then jump back 4 spaces to 76. 19 x 4 = 76
How could you use this idea of multiplying by 20 and adjusting to solve these problems?: 21 x 6; 19 x 8; 21 x 4
Can you use the idea of adjusting by one to calculate multiples of 29 and 31?
Division (2 digit by 1 digit)
6 cupcakes fit in a box. How many boxes can be filled with 85 cupcakes?
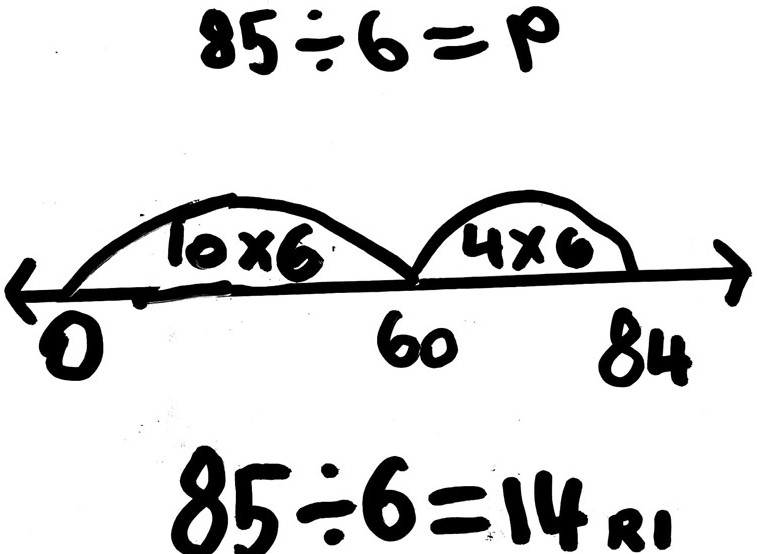
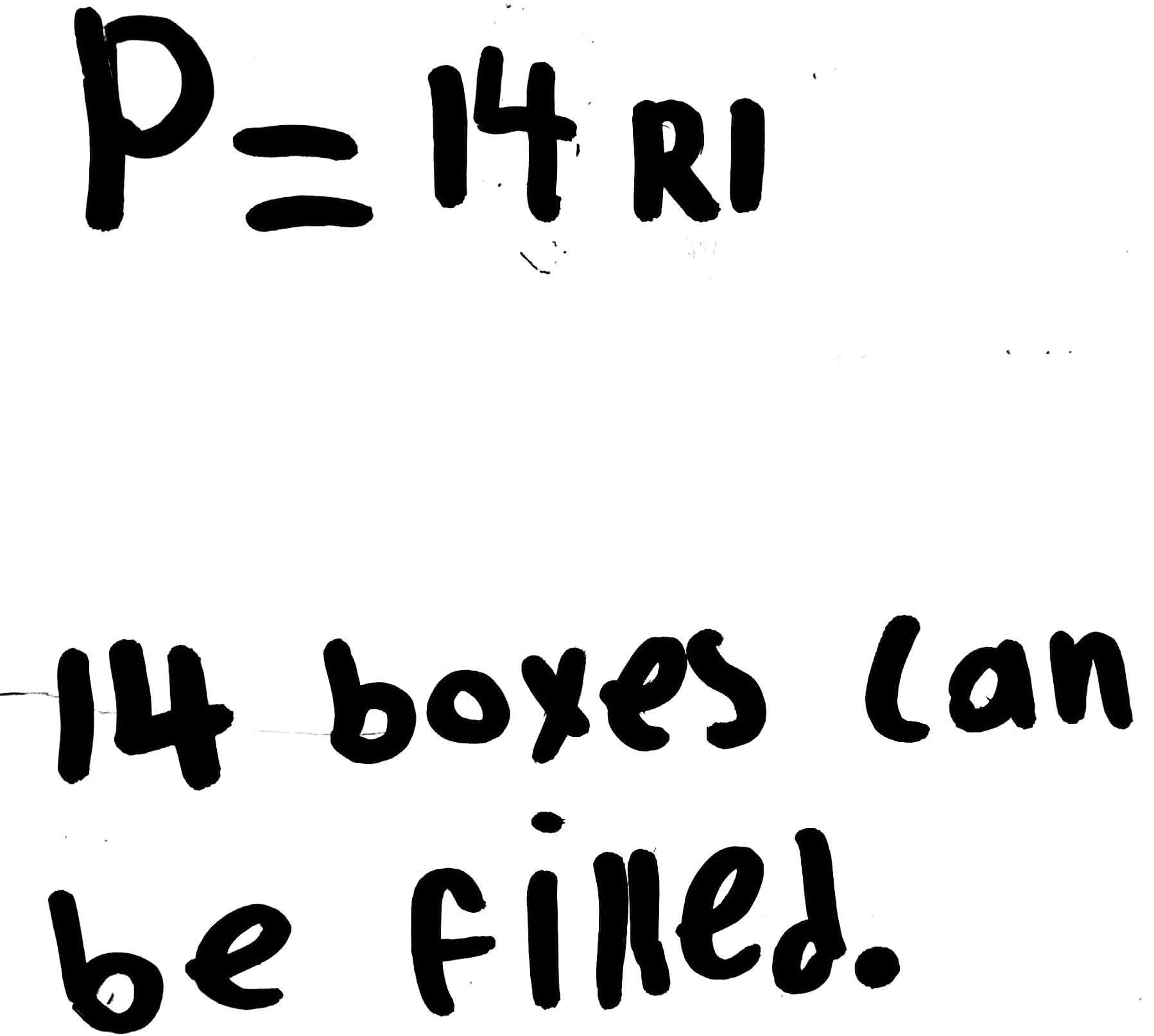
To solve this problem we could count up in sixes one at a time but that would not be efficient. This student thought about easy, but larger 'chunks' of 6 such as 10 x 6 (60) and
4 x 6 (24), leaving 1 remaining cupcake. 14 boxes can be filled.
Division (3 digit by 2 digit)
If a box holds 28 apples, how many boxes can be filled with 350 apples?
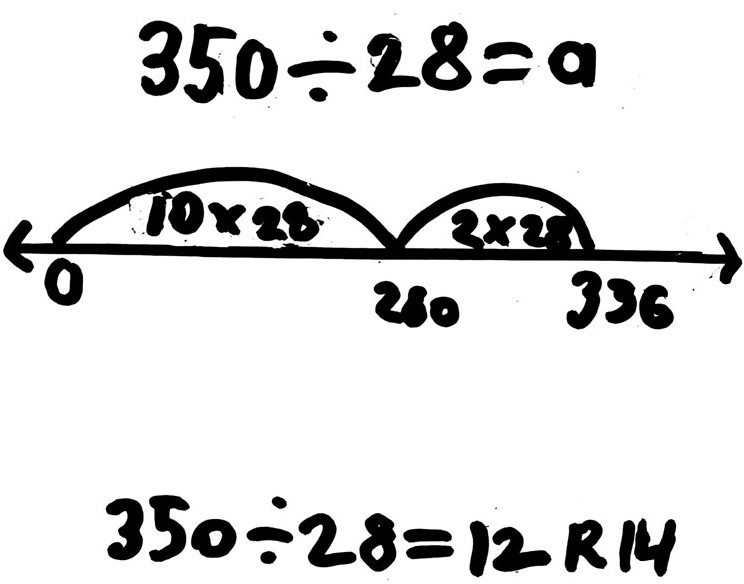
To solve this problem this student thought about ‘friendly’ chunks of 28 such as 10 x 28 (280). First, a jump is made to show 10 chunks of 28 (280), then two more ‘chunks’ of 28 (56) are added mentally to reach 336. This leaves 14 apples which is not enough to fill another box, so 12 boxes can be filled.
Given ongoing opportunities to use the empty number line students will begin to solve problems mentally by picturing the empty number line in their heads. Regular use increases students’ confidence in their ability to use numbers flexibly and leads more easily towards mental calculations without paper.