Subtraction Strategies

The anchor charts on this page provide examples of five subtraction strategies that can be used to mentally solve multi-digit subtraction problems efficiently and effectively, namely Use Doubles, Make a Ten,  Add Up, Removal and Keep a Constant Difference.  Understanding of these subtraction strategies can have a far ranging impact as they can all be extended from one-digit numbers to multi-digit numbers, fractions and decimals. As seen below, an open number line can be used as a visual model for several of these subtraction strategies.  When using open number lines it is important to note that they do not have a scale and therefore are not intended as accurate measures of units but are roughly proportional.

Free Downloads: Copies of the subtraction strategy charts shown below can be downloaded here. For addition strategy charts see here.

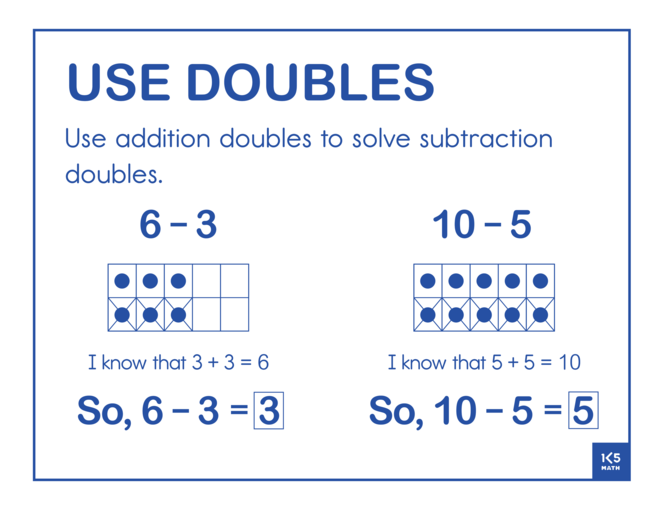
The Use Doubles subtraction facts are related to the Use Doubles addition facts. Once students understand that if they know the addition fact 9+9=18 then they also know the subtraction fact 18-9=9, they can begin to apply this strategy to 'near doubles' subtraction problems such as 11-5, 42-20 or 298-150.

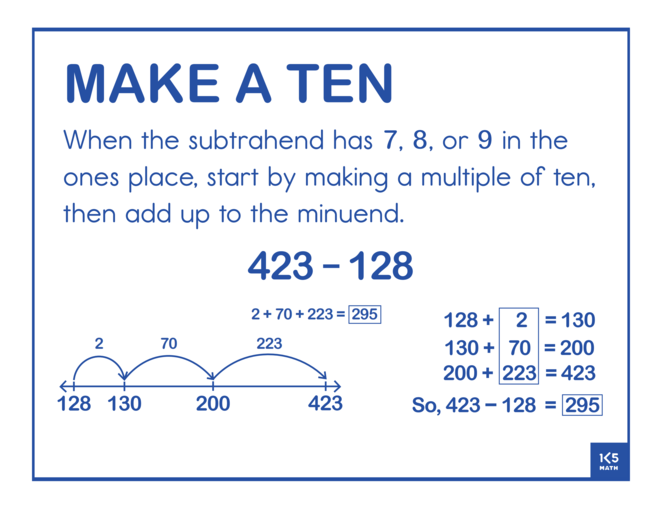
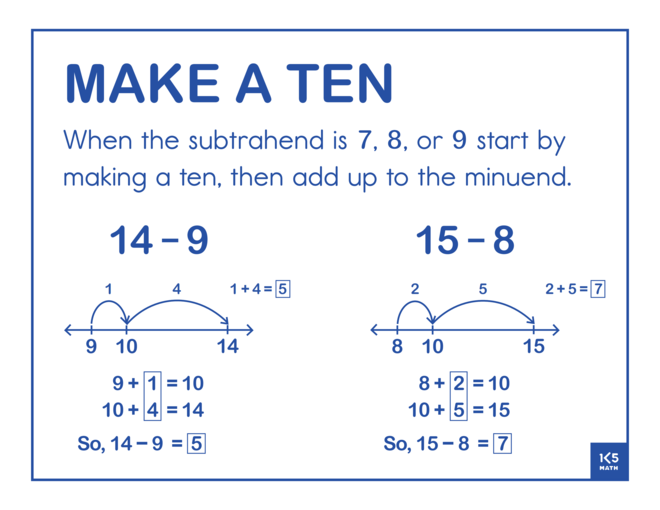
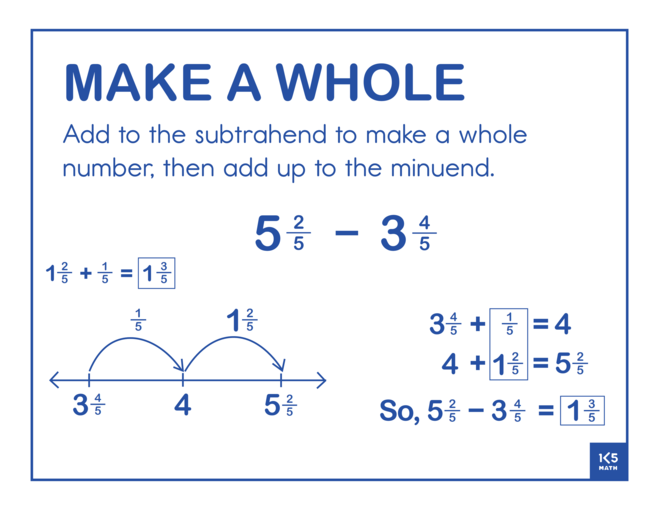
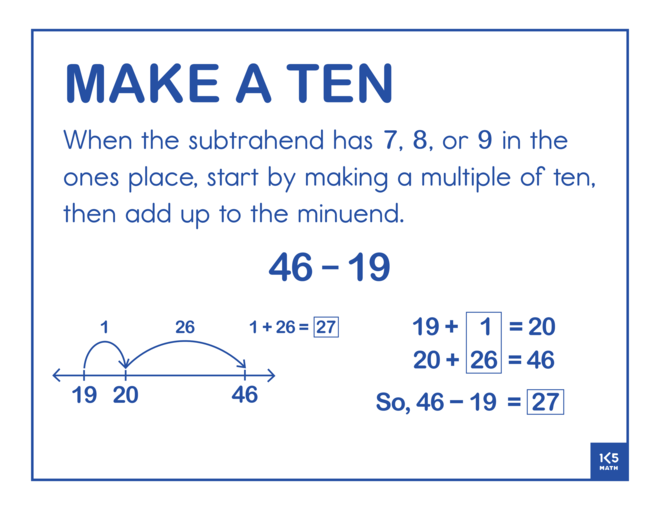
The Make a Ten strategy for subtraction is built on the understanding that any subtraction problem can be represented as a missing addend problem because of the inverse relationship between addition and subtraction. By starting at the subtrahend a problem such as 14 - 9 becomes 9 + ? = 14. This is a useful mental strategy for figuring out the difference when the subtrahend is close to ten, or a multiple of ten. For example, for 85 - 37 a student might think '37 and 3 makes 40, and 45 makes 85. 3+45=48 So, 85-37=48.' Fluency work reviewing facts of ten or how many more to get to a multiple of ten/hundred can make for a useful warm up prior to a Number Talk focusing on this strategy.

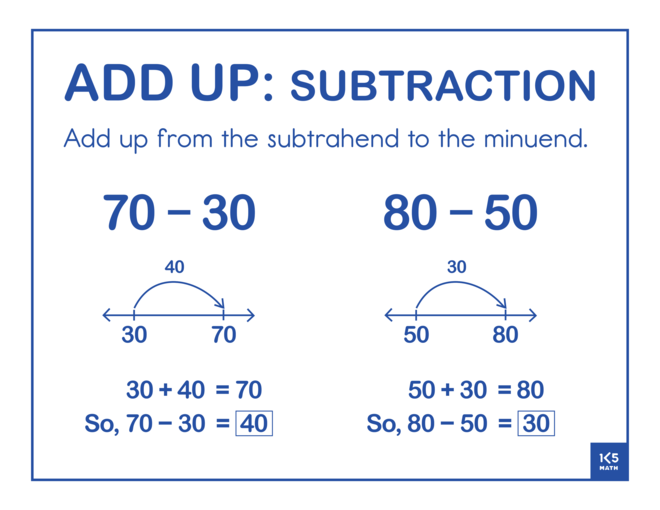
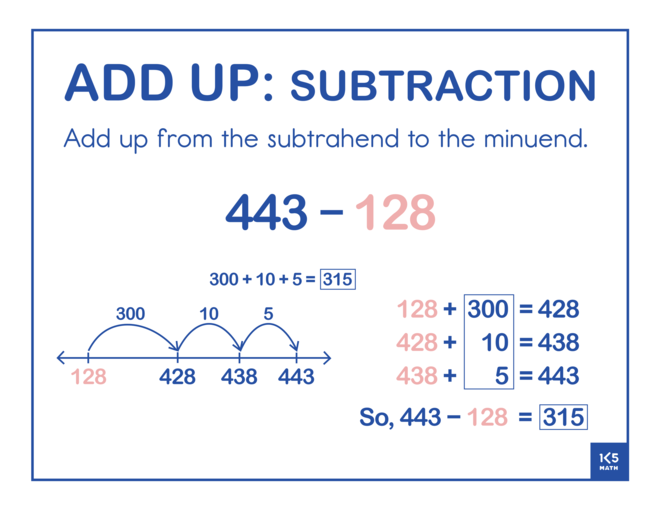
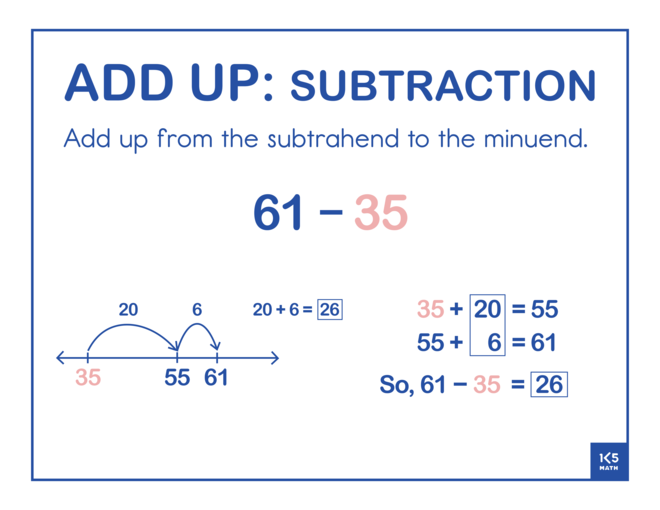
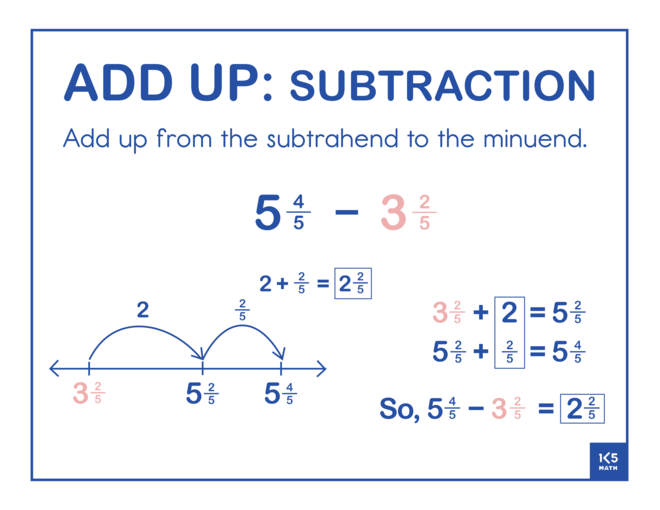
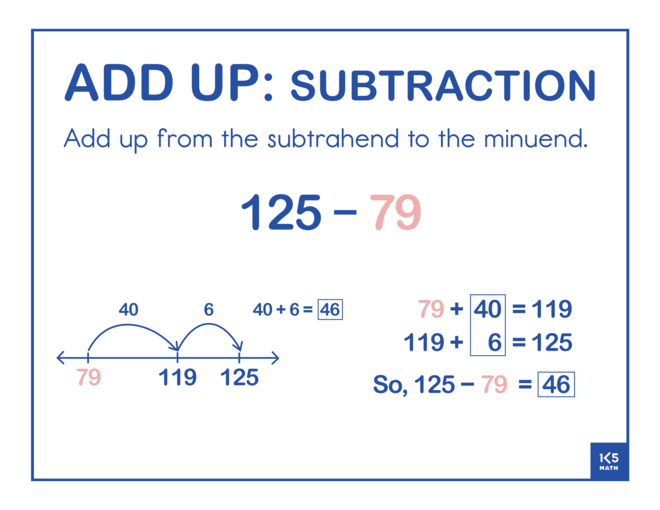
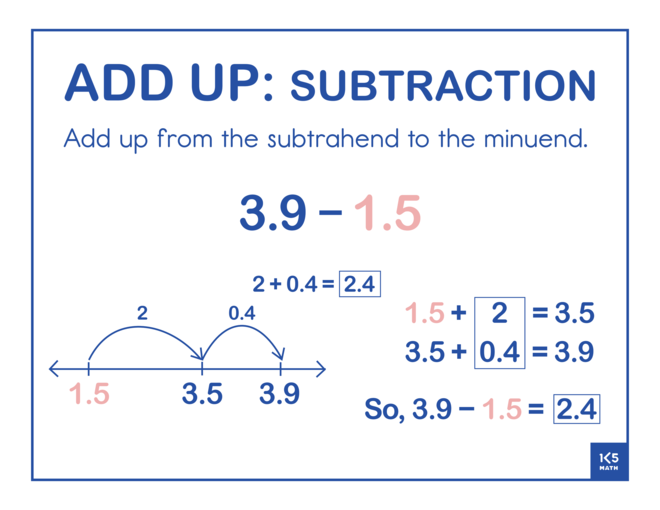
The Add Up strategy involves adding up from the number being subtracted (subtrahend) to the whole (minuend). Start by selecting problems where the minuend and subtrahend are close together (e.g. 57 - 53 or 332 - 326) to build an understanding of subtraction as the distance between two numbers. Regularly asking students to share and compare the jumps they made will gradually lead to students  making more efficient jumps when working with larger numbers. Using story contexts that look at how much more is needed to get to an amount may also help students understand that the goal is to find the difference between two numbers (e.g.  Lia's goal is to practice her violin for 240 minutes per week. She has already practiced for 175 minutes this week. How much longer does she need to practice to meet her goal?)

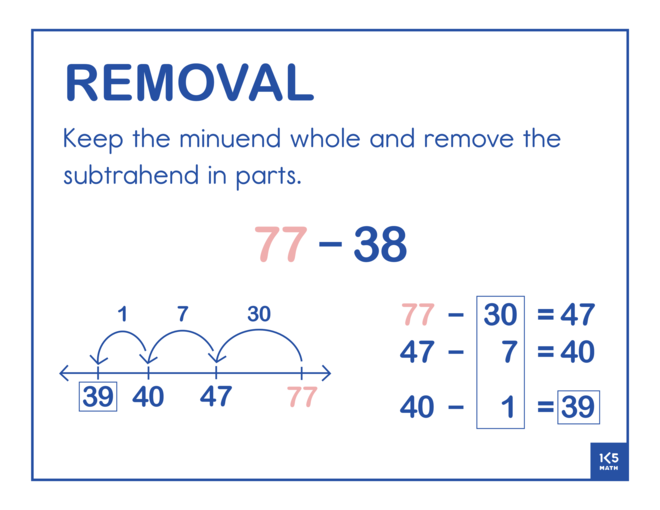
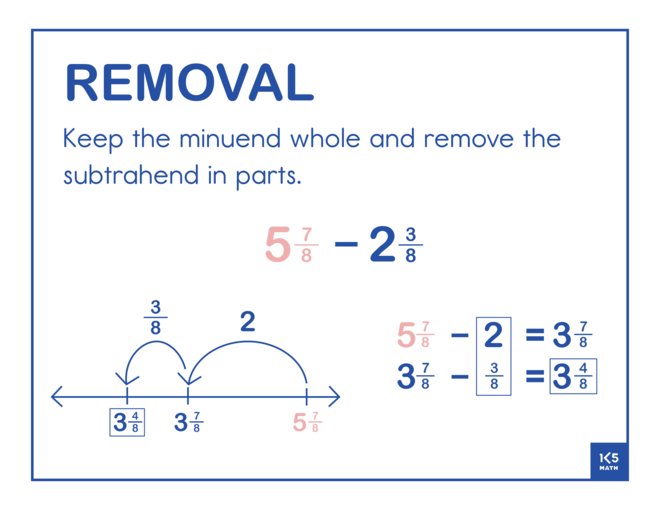
The Removal strategy involves decomposing the subtrahend and removing it in parts to make a series of smaller and easier problems. In order to remove the correct amount students need to keep track of how much they subtract.

Keep a Constant Difference involves adjusting both the minuend and subtrahend by the same amount. In order to use this strategy successfully students need to understand that if you add or subtract the same number from both the minuend and the subtrahend, the difference, or distance between the two numbers, will not change.  Using an exploration in which students work with a partner to explore whether keeping a constant difference will always work can be a good way to introduce this strategy as it it not one that students tend to come up with on their own. Once this strategy is understood many students find it to be useful as both a mental strategy and when solving subtraction problems involving regrouping across zeros using pencil and paper. For example, a problem such as  5,000 - 2,384 becomes an easier problem to solve after subtracting one from both the minuend and subtrahend (4,999 - 2,383) because regrouping is no longer required.