Let's Build Spatial Reasoning

Tangram Task Cards from Building Spatial Reasoning eBook

The National Council of Teachers of Mathematics (2000) acknowledges the importance of identifying shapes, but also stresses that a child’s construction of an understanding of shapes goes beyond just rote memorization of shape names. Children need to engage in activities that build spatial reasoning, the cognitive process involved in constructing mental images of shapes and predicting the effect of rotating or flipping a shape in one’s mind. Spatial abilities include being able to think about how objects look from different angles, how positions of objects relate to each other in space (e.g. the ball is on top of the table, the shoe is under the table, and the dog is in front of both) and how parts of an object fit together (e.g. being able to predict that if two triangles are put together in a certain way they will make a rectangle). These skills are essential to daily living. How would you rate your own skills at packing a suitcase, deciding which container to use to put the leftovers in after a family dinner, or picturing in your mind how to rearrange the furniture in your living space? When the need for parallel parking arises, how do you decide if the car you are driving will fit between two parked cars? How do you rate your ability to follow a map on your phone or find your way around a supermarket, shopping mall or zoo? Distances, directions and locations all rely on spatial reasoning abilities as do many other tasks we complete on a daily basis.

Along with its obvious importance in everyday life, research suggests that young children's abilities to engage in geometric thought and spatial reasoning can support their overall mathematical and cognitive development. Spatial thinking abilities can predict students’ success in other areas of mathematics, such as part-whole relationships, fractions, area, volume, proportional thinking, coordinate graphing and algebraic reasoning. For example, children's spatial scaling skills have been shown to correlate with their ability to accurately position numbers on a number line. Similarly, children who demonstrate strong mental rotation skills have been shown to be more successful at missing number problems such as ? + 3 = 5. The good news is that research shows that spatial reasoning skills can be improved with practice. Regular experiences with hands-on manipulatives such as pattern blocks, tangrams and geoboards provide opportunities to explore what happens when we compose various shapes to create new shapes and decompose shapes to look at the smaller shapes within them. Working with these materials supports the development of both spatial reasoning and problem solving as they require that we must think about which way to place individual pieces and transform them in a way such that they fit together to form a whole.

Providing both structured and unstructured opportunities for children to build spatial reasoning skills is important. During unstructured, or free play, children build designs of their own choice. During structured play children attempt to make a particular structure from a model. These tasks call on different processes. Free play invokes one’s imagination and ability to produce complex relations without prompting, while structured play calls upon the ability to analyze a spatial representation to create a predefined model. As children work with manipulatives to compose and decompose shapes, encourage them to go beyond merely naming shapes to talk about the defining properties, e.g. “These are both triangles, because all triangles have 3 sides and 3 angles.” Some possible questions to ask include:

Can you show me how you filled this shape?
What would fit there? (pointing to an angle in the frame)
What will happen if you turn/rotate this shape?
If we turn this, is it still the same shape?
Can you build that another way using more/less shapes?
How many different ways can you fill this shape outline?
What other shapes have four sides/ three vertices? etc.
What do you notice about the lengths of the sides? Are they the same or different?
Can you substitute a rhombus/trapezoid/hexagon for any of the shapes you used?
What is the same/different about these two triangles?
How are squares and rectangles different? What about a triangle and rhombus?

Pattern Block Task Cards from Building Spatial Reasoning eBook

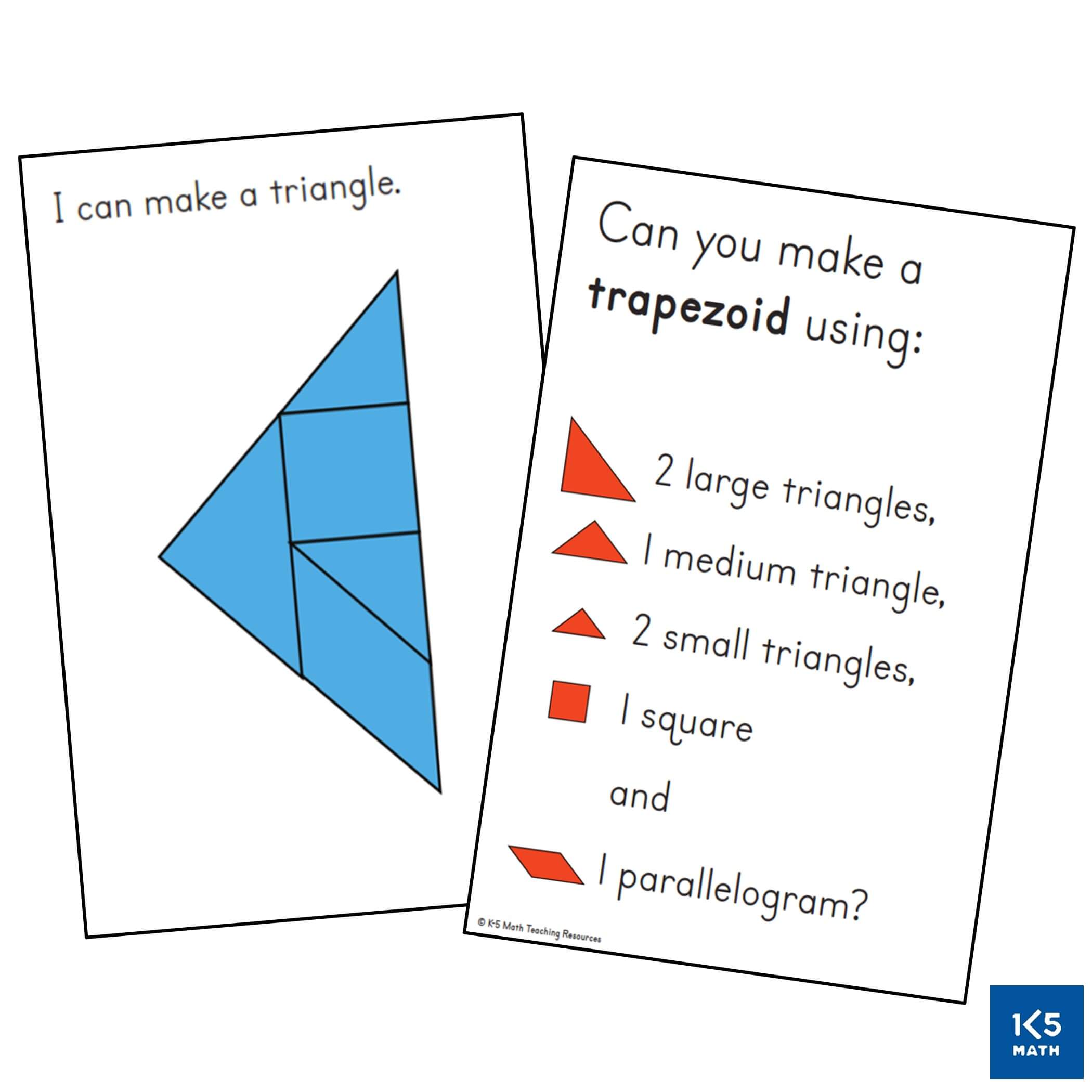
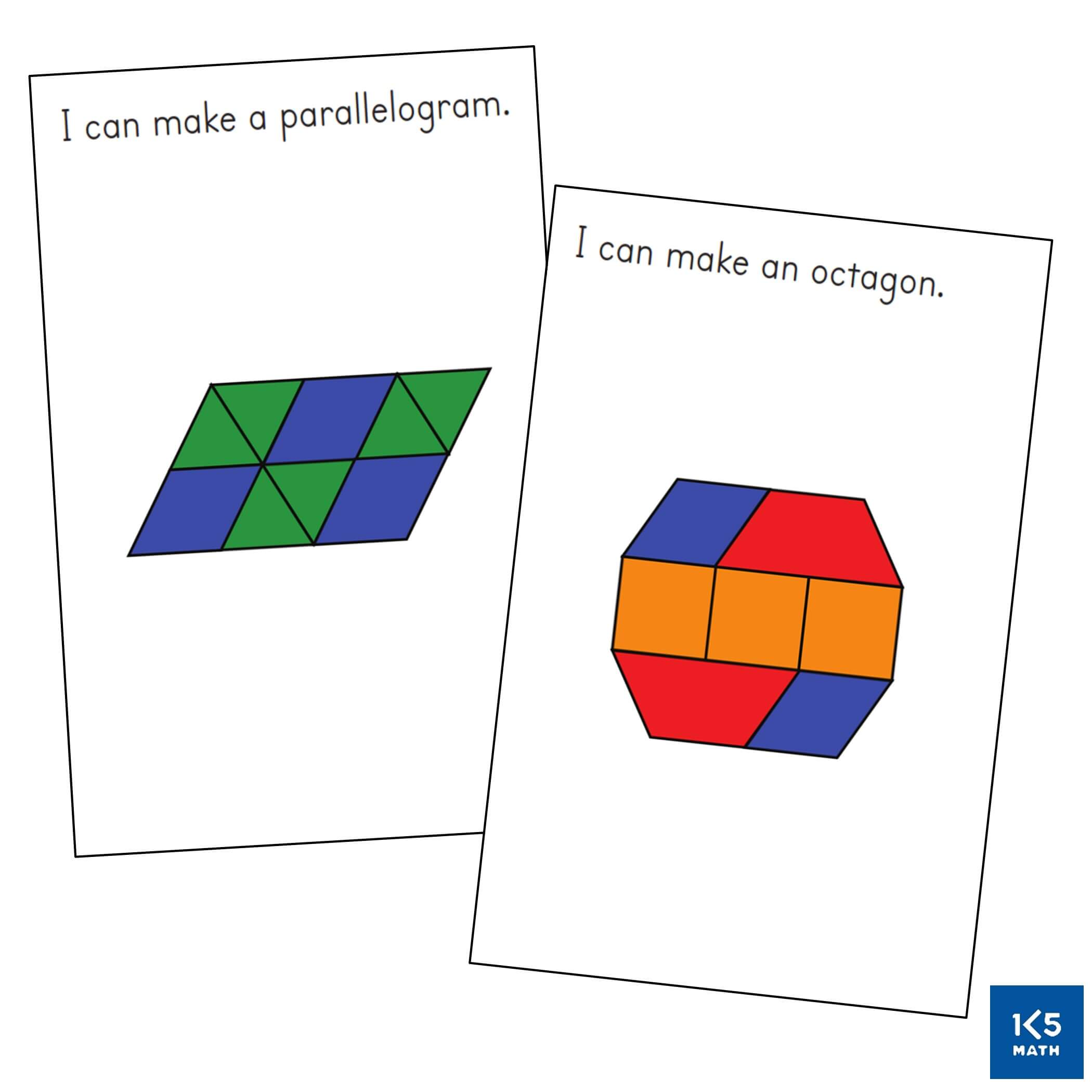
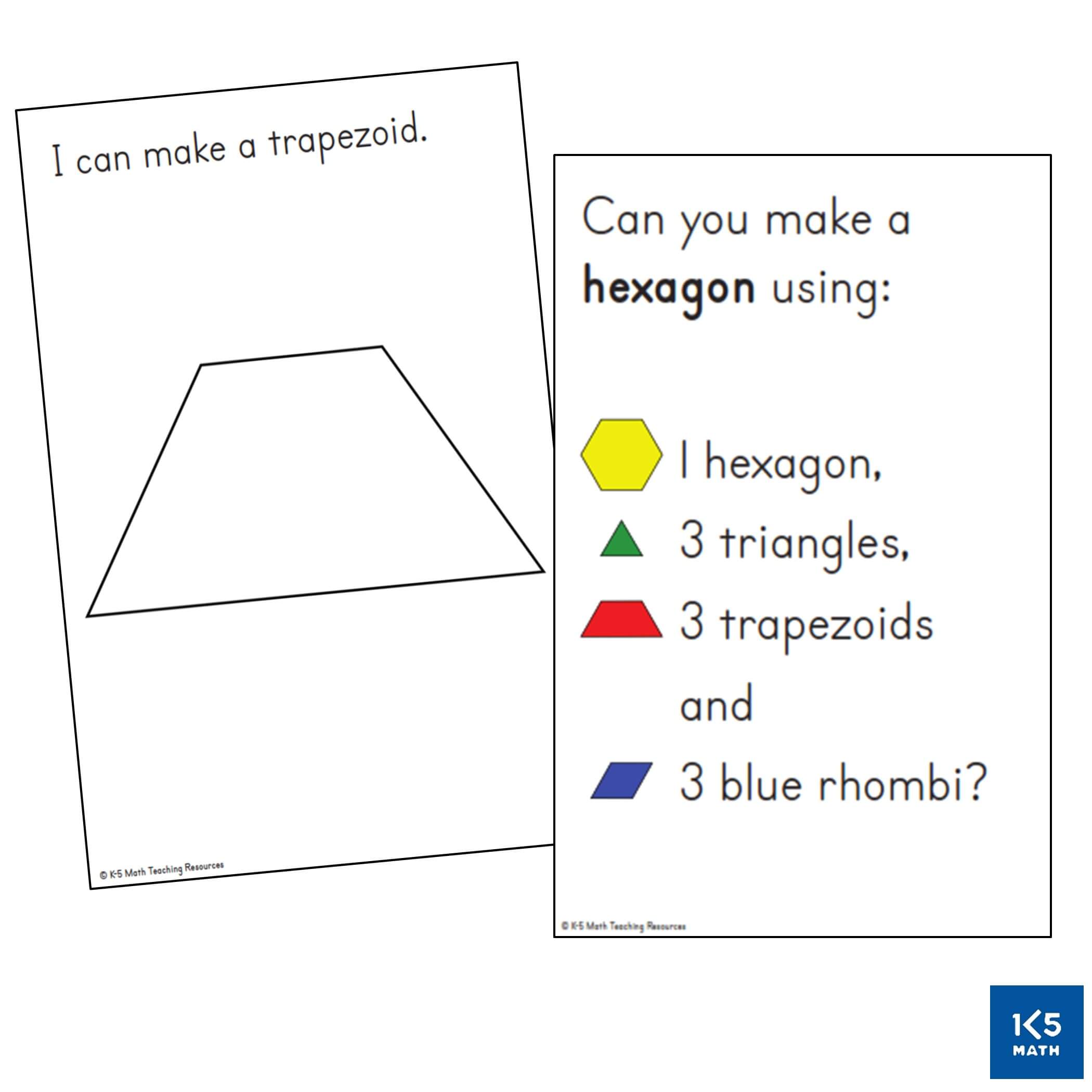
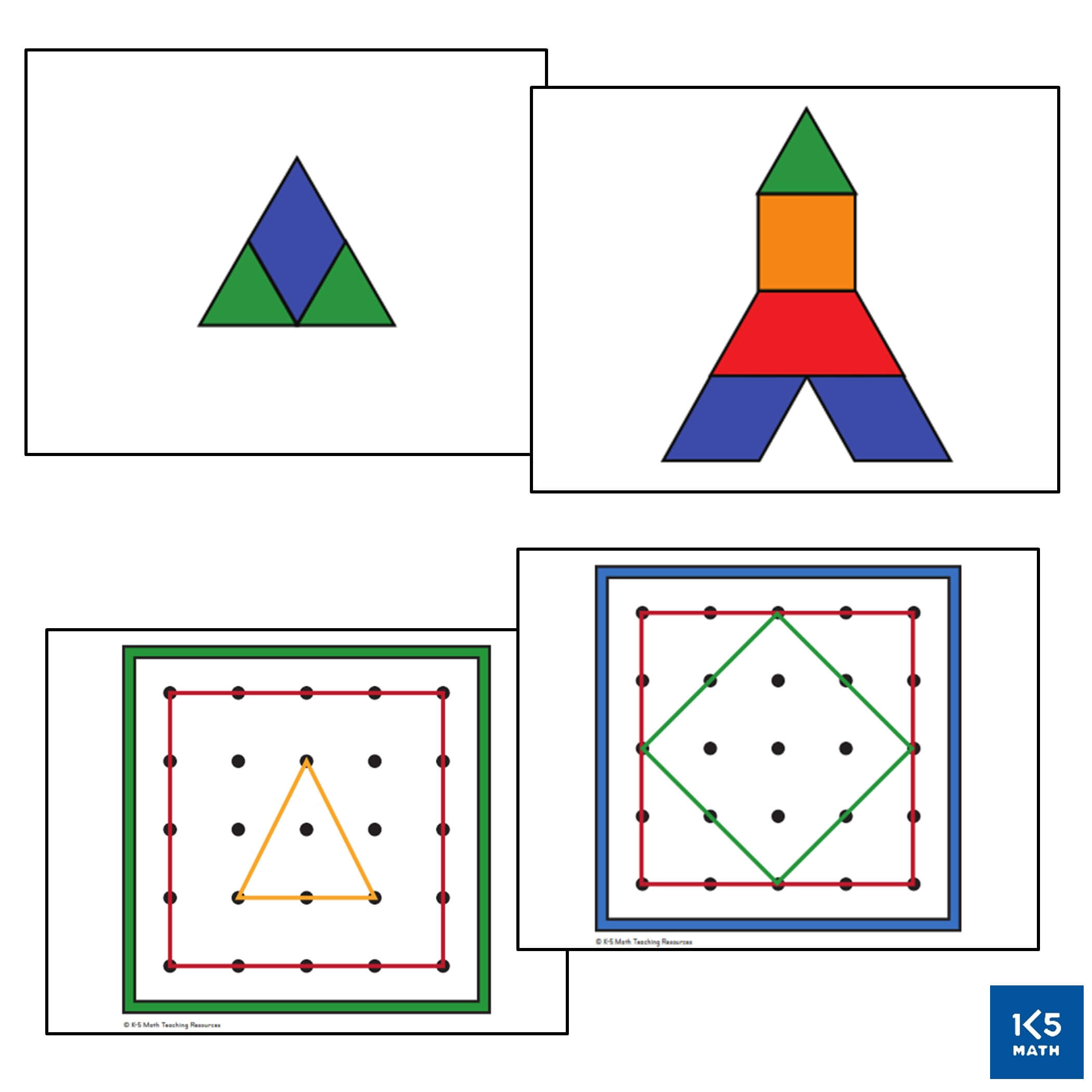
When working with pattern blocks and tangrams begin with task cards that provide scaffolding in the form of internal shape and color clues for children to see how shapes can be put together to make a larger shape. Young children can either build directly on top of the card or alongside it. Children need to understand that a triangle has certain defining properties and a square has others and that these properties are invariant over changes in size, orientation or color. Models of both regular and irregular shapes should be provided to make explicit the defining properties of each shape so that children can explain why a hexagon is a hexagon even if it is not the prototypical hexagon seen in a pattern block set. As students are ready, move to more complex cards that show only the outline of a shape without any internal shape clues, and later those that simply name the shapes used to build a larger shape. Task cards without any internal clues can be challenging and often require trial and error. Encourage perseverance (“I can see that you are thinking very carefully about where to place each shape.”) and make suggestions as needed (“Sometimes when I get stuck, I take out some blocks/tans and try different ones.”)

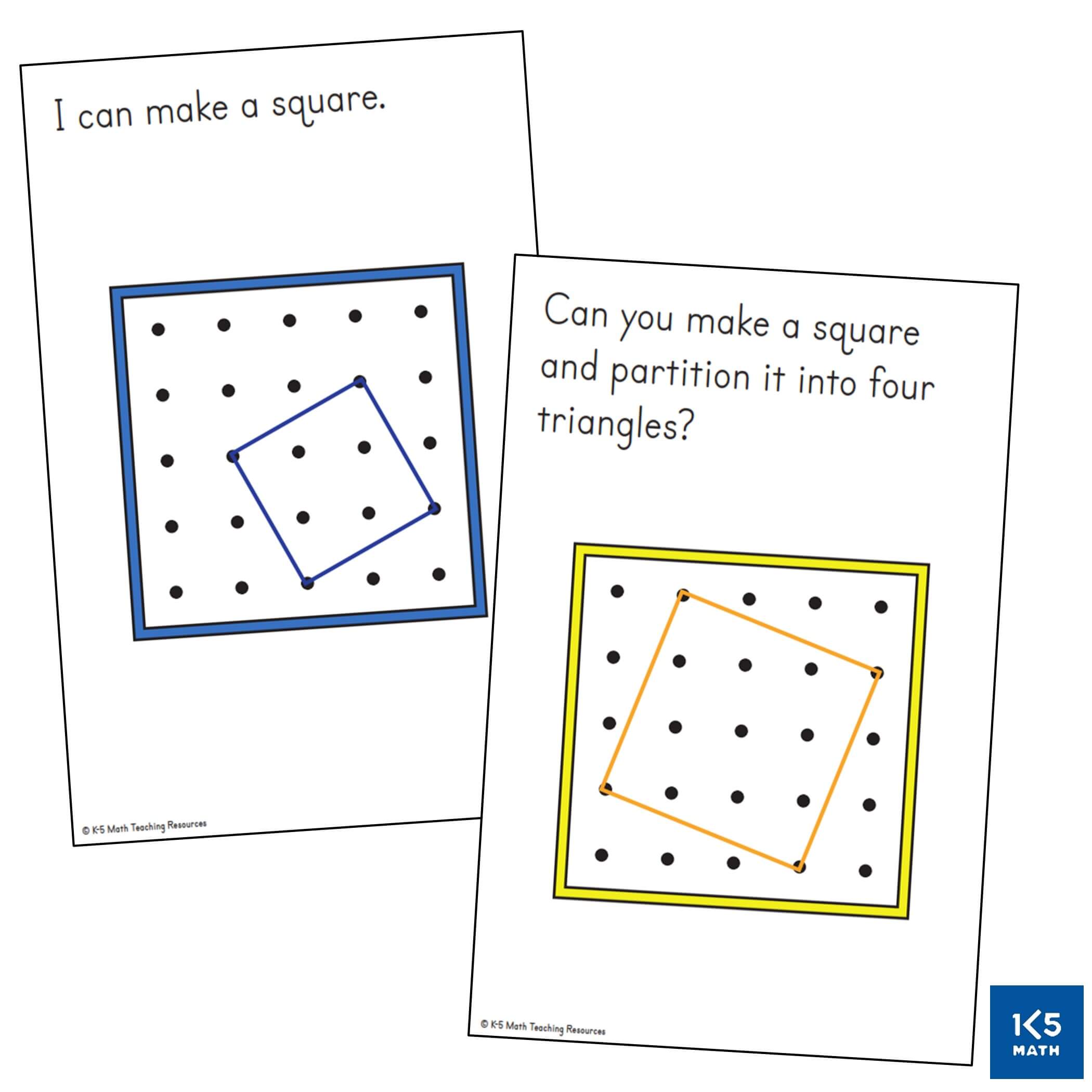
Geoboards are an often underutilized hands-on learning tool in classrooms that can provide an engaging way for students to explore geometric properties of shapes and develop an understanding that the properties of a shape do not change when the orientation changes (e.g. a square does not always have a horizontal base). This is a common misconception with young learners (and sometimes older students) who may think that a rotated square is not a square because it looks different from their visual image of a square. This may be because children are more likely to have seen shapes drawn upright than tilted at an angle in picture books, puzzles, games and commercially made charts from a young age. Our job is to help students expand their visual definitions of shapes so that they are better able to recognize and describe them. Differentiated tasks providing opportunities for students to build, partition and draw shapes in a variety of orientations, such as the geoboard task cards on the right, can assist with this.

Geoboard Task Cards from Building Spatial Reasoning eBook

Building skeletal models of 3D shapes using toothpicks and frozen peas

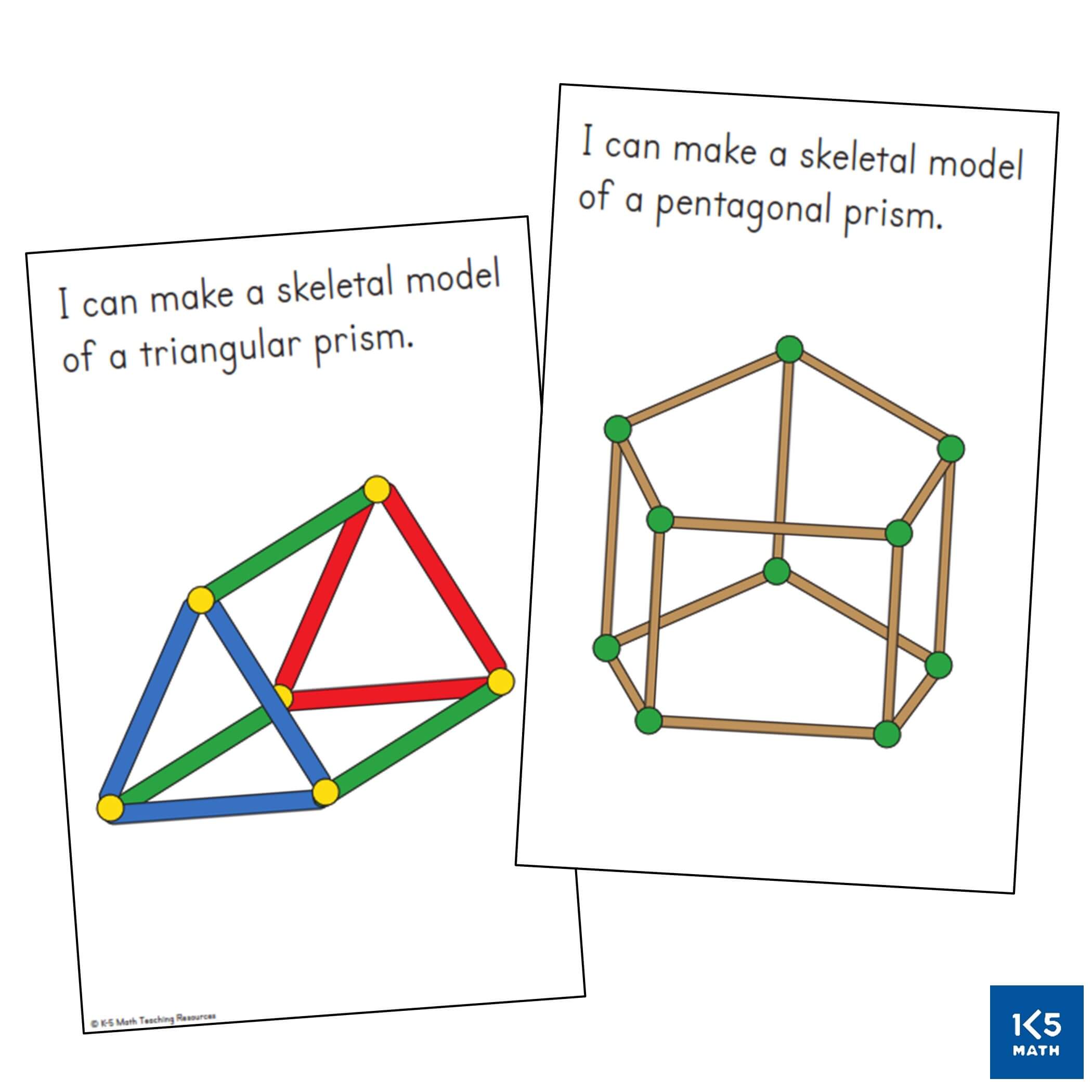
Building skeletal models is always a popular activity that gets students thinking and talking about the properties of three-dimensional shapes. A skeletal model shows the outline or framework of an object. The edges of the model can be made from toothpicks, craft sticks or straws. We like to use frozen peas to create vertices and join edges together when using toothpicks but small balls of playdough, or plasticine, work just as well.

The ability to picture an image in one's mind is an important part of geometric reasoning. Quick Images with pattern blocks, tangrams and geoboards encourage students to pay close attention to the geometry they see when they briefly view a geometric figure, or design, and then build it from the mental image formed. Follow the steps below to introduce the Quick Images routine. Once students are familiar with the routine it can become a math center task for partner work.

1. Turn over a Quick Image card for 3 seconds. Ask students to try and hold the image in their mind.
2. Students build what they saw from memory.
3. Flash the image again to allow students to notice additional features.
4. Show the image a third time and discuss the mental images students formed by asking questions such as:

What did you first see when you looked at the image?
What did you miss the first time you looked at the image?
What strategies did you use to remember what you saw?
How did you revise your shape/image after seeing it again?

Quick Images with pattern blocks, tangrams and geoboards can be used to build geometric reasoning.

Well developed spatial reasoning skills are crucial for careers in science, technology, engineering, and mathematics (STEM) and many other occupations that require critical thinking and problem-solving on a day-to-day basis. How much time does your math curriculum devote to hands-on tasks and rich math talk about shapes, their attributes and properties?