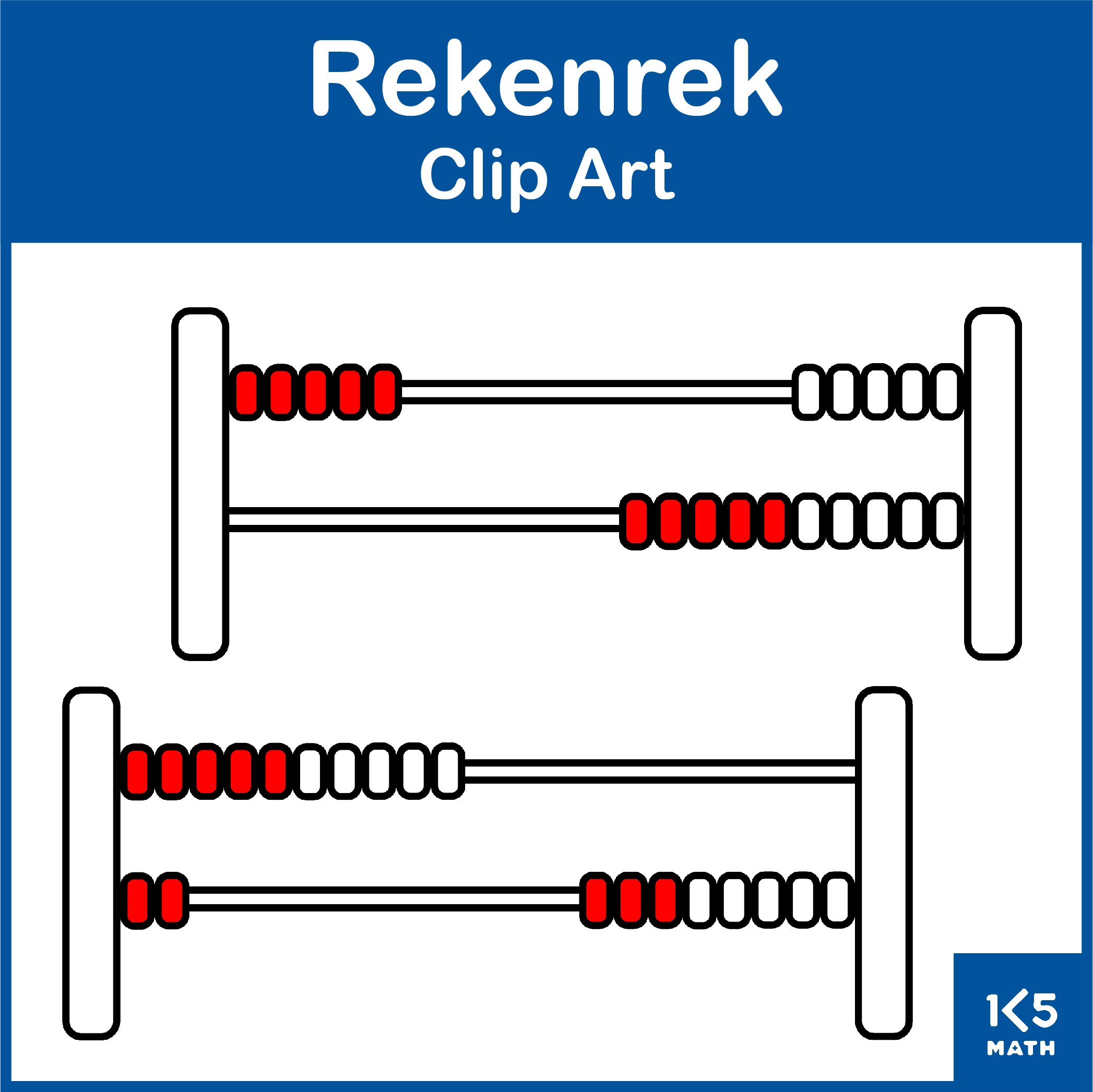
Rekenrek Activities
In the realm of early mathematics education, fostering number sense and understanding place value are foundational skills. However, these concepts can often be abstract and challenging for young learners. One effective tool that many educators utilize to make these concepts more tangible and accessible is the rekenrek. The rekenrek, also known as the arithmetic rack, was designed by Adrian Treffers, a mathematics curriculum researcher at the Freudenthal Institute in Holland, to support the natural development of number sense in children. Smaller versions consist of two rows of 10 beads, while larger versions have ten rows of ten beads. Each row has five red beads and five white beads. This structure helps students visualize numbers in terms of fives and tens, laying a solid foundation for understanding place value. Using 5 and 10 as anchors for counting, adding and subtracting is obviously more efficient than one-by-one counting. The rekenrek provides learners with the visual models they need to discover number relationships and develop a variety of addition and subtraction strategies, including doubles plus or minus one, making tens, and compensation, thereby leading to automaticity of basic facts.
Benefits of Using Rekenreks
➡️Concrete Representation: Rekenreks offer a physical representation of numbers, making abstract mathematical concepts more tangible for young learners. Students can physically move beads to manipulate numbers, aiding in conceptual understanding.
➡️Developing Number Sense: By using rekenreks, students develop a deep understanding of number relationships and operations. They can visually see how numbers combine and decompose, facilitating mental math strategies and fluency.
➡️Place Value Understanding: The organization of beads in groups of five and ten helps students grasp the concept of place value. They learn to recognize that ten ones make a group of ten, laying the groundwork for understanding two-digit numbers and beyond.
Possible Rekenrek Activities
💡Meet the Rekenrek: Begin by asking children what they notice about the rekenrek. Then introduce the ‘start position’(all beads over to the far right) and have them practice sliding beads in groups rather than one by one “Put your beads in start position. Now, without touching the beads, count the first three beads in your mind. On the count of three, slide all three beads at once across the string. One… two…three!” Repeat with other numbers.
💡Show me 0-10: Say a number, or hold up a numeral card (0-10). Ask students to show the given number by moving the beads with one push.
💡Show me 11-20: As above but ask students to show the given number of beads using only two pushes.
💡Quick Images to Build Subitizing Skills: Push some beads across and display them briefly before covering them with a piece of cloth or card. Ask, “How many beads did you see? How do you know?” Asking children to draw or write what they saw on a dry erase board ensures that everyone is actively involved and serves as a quick assessment. If using a 100 bead rack gradually add rows until you are displaying quick images to 100. This can be extended by asking students to show the number that is one more/one less/ten more/ten less than/double the number flashed.

💡Building Missing Addends: Ask a student to be your partner. Tell the class that you and your partner are going to build the number 6 as a team. You will move beads on the top row and your partner will move beads on the bottom row. “I am going to slide 4 beads to the left on the top row. Now in one move, you slide beads on the bottom row to build the number 6.” Pair students up and have them turn over the top card in a stack of numeral cards and work with their partner to build that number in as many different ways as possible. Begin with cards 1-10, later increase to 1-20. An arithmetic rack with ten rows can be used with students who are ready to represent numbers larger than 20.
💡Finding Different Ways to Make a Given Number: Initially use only the top row of beads. Cover the bottom row with a folded sheet of card or piece of fabric. Begin by sliding the red beads to the left and the white beads to the right on the top row of the rekenrek. Choose a number to build. “Let’s see how many ways we can build 6 by sliding beads from each side to the middle. What if I slide 4 red beads from the left and 2 white beads from the right. Does that make 6 beads? Can you think of another way to make 6? Record the different ways 6 can be built. This activity should be repeated many times using different numbers from 1-10. Once children are confident using the top row, combinations can be found using both the top and bottom rows. Children can record the different ways they find to build the given number.
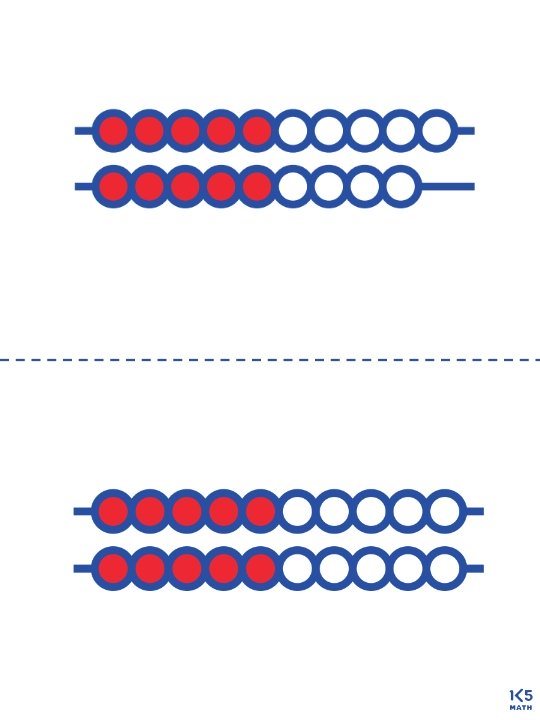
|
Click on the blue text below to download prompt cards and flashcards to use during mental math sessions. Print on cardstock and place on a ring for teacher reference or place in a math center for children to use when working with a partner. b) Rekenrek Cards (1 - 20) |
Interested in using rekenreks in your class but don't have the budget to buy a class set? See these instructions on how to make a class set for just a fraction of the price of store bought models. |
Possible Math Journal Tasks:
🟢Show 5: How many different ways can you show 5 on your rekenrek? (repeat with different numbers)
🟢Doubles: How many different doubles facts can you show on your rekenrek? Record.
🟢Near Doubles: How many different ‘near doubles’ can you show? Record.
🟢Turn Around Facts: Show an addition fact. What would the turn around fact look like? Repeat.
Number Stories: Have children use individual arithmetic racks as a tool to solve various types of addition and subtraction number stories. This may be used as a journal or oral activity, with the focus on children explaining their strategy for solving the problem. Be sure to include open-ended problems that have more than one solution that children can model on the arithmetic rack, such as the following:
➡️There were 8 children on a bunk bed. Some were on the top bunk and some were on the bottom bunk. How many children were on the top bunk? How many children were on the bottom bunk? Show as many different solutions as you can.
➡️There were 12 passengers on a double-decker bus. Some passengers were on the top deck and some were on the bottom deck. How many passengers were on the top deck? How many passengers were on the bottom deck? Show as many different solutions as you can.
The below two work samples were completed by a Kindergarten student who represented her work very clearly on the unlined pages in her Math Journal using pictures, numbers and words. To begin with some Kindergarten students may find it difficult to represent their work on paper. Having recording paper available for children who choose to use it is one way to scaffold early attempts at drawing.
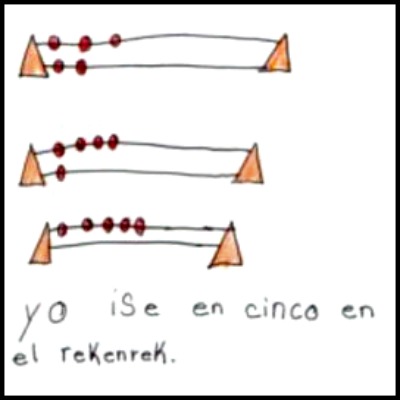
Incorporating rekenreks into kindergarten and first-grade classrooms is an effective way to build number sense and place value understanding. Through hands-on exploration and manipulation of beads, students develop a deep conceptual understanding of mathematical concepts. From counting and cardinality to addition, subtraction, and place value, rekenreks offer a versatile tool for engaging young learners and laying a solid foundation for future mathematical success. By integrating these activities into the curriculum, educators can create meaningful mathematical experiences that empower students to become confident and proficient mathematicians.
Amazon Associates Disclosure
K-5mathteachingresources.com is a participant in the Amazon Services LLC Associates Program, an affiliate advertising program designed to provide a means for sites to earn advertising fees by advertising and linking to Amazon.com