4TH GRADE NUMBER
This page provides sample downloads from some of the resources in 4th Grade Mega Math Bundle aligned with the 4th Grade Number Common Core State Standards. Try some of the samples listed in blue below each standard or download the bundle and have instant access to hundreds of easy-prep, engaging resources to simplify your math lesson planning and make active engagement through hands-on math instruction an integral part of your fourth grade classroom.
OPERATIONS AND ALGEBRAIC THINKING
Use the four operations with whole numbers to solve problems
4.OA.A.1 Interpret a multiplication equation as a comparison, e.g., interpret 35 = 5 x 7 as a statement that 35 is 5 times as many as 7 and 7 times as many as 5. Represent verbal statements of multiplicative comparisons as multiplication equations.
4.OA.A.2 Multiply or divide to solve word problems involving multiplicative comparison, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem, distinguishing multiplicative comparison from additive comparison.
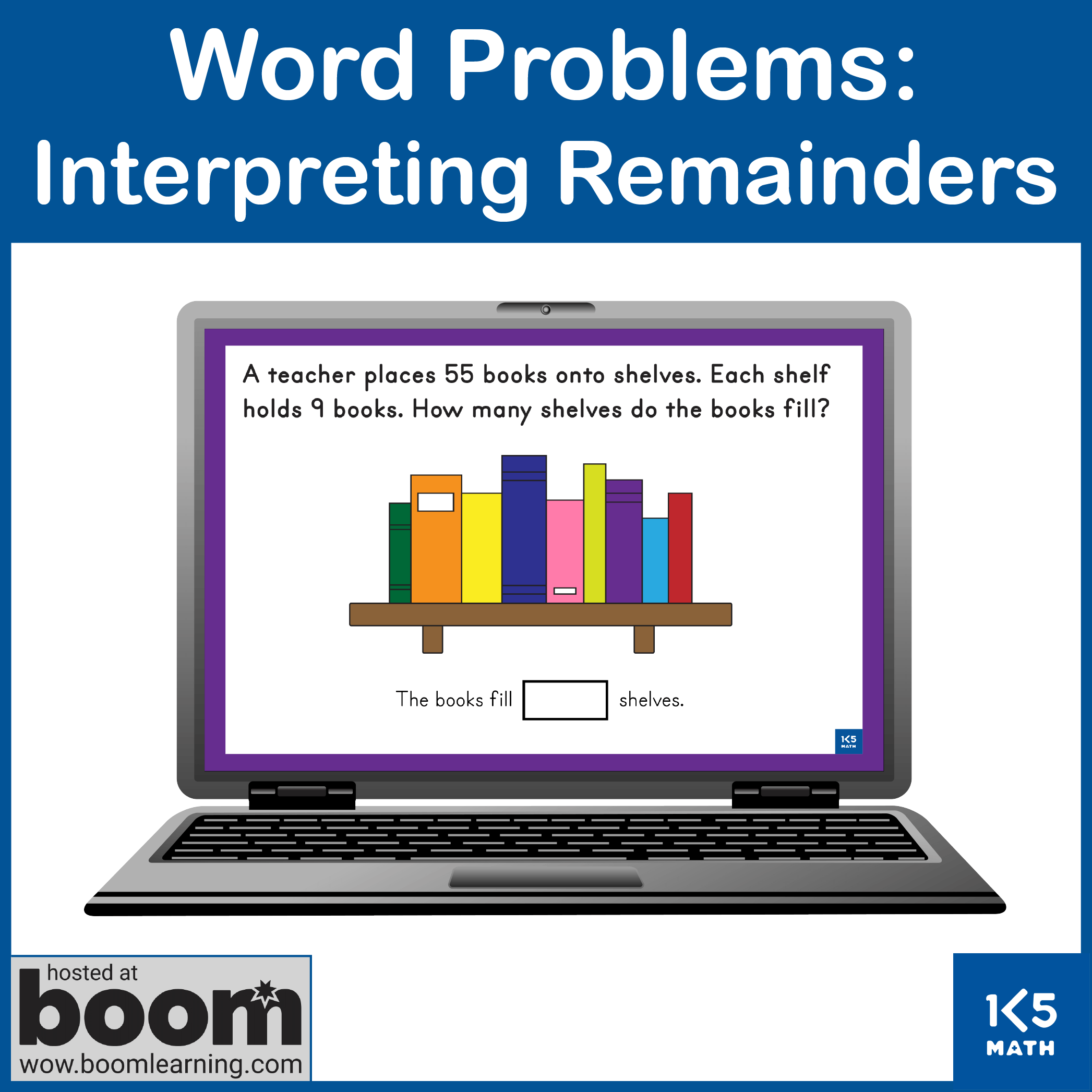
4.OA.A.3 Solve multistep word problems posed with whole numbers and having whole-number answers using the four operations, including problems in which remainders must be interpreted. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding.
Gain familiarity with factors and multiples
4.OA.B.4 Find all factor pairs for a whole number in the range 1-100. Recognize that a whole number is a multiple of each of its factors. Determine whether a given whole number in the range 1-100 is a multiple of a given one-digit number. Determine whether a given whole number in the range 1-100 is prime or composite.
Generate and analyze patterns
4.OA.C.5 Generate a number or shape pattern that follows a given rule. Identify apparent features of the pattern that were not explicit in the rule itself. For example, given the rule “Add 3” and the starting number 1, generate terms in the resulting sequence and observe that the terms appear to alternate between odd and even numbers. Explain informally why the numbers will continue to alternate in this way.
NUMBER AND OPERATIONS IN BASE TEN
Generalize place value understanding for multi-digit whole numbers
4.NBT.A.1 Recognize that in a multi-digit whole number, a digit in one place represents ten times what it represents in the place to its right. For example, recognize that 700÷70=10 by applying concepts of place value and division.
4.NBT.A.2 Read and write multi-digit whole numbers using base-ten numerals, number names, and expanded form. Compare two multi-digit numbers based on meanings of the digits in each place, using >, =, and < symbols to record the results of comparisons.
4.NBT.A.3 Use place value understanding to round multi-digit whole numbers to any place.
Use place value understanding and properties of operations to perform multi-digit arithmetic
4.NBT.B.4 Fluently add and subtract multi-digit whole numbers using the standard algorithm.
4.NBT.B.5 Multiply a whole number of up to four digits by a one-digit whole number, and multiply two two-digit numbers, using strategies based on place value and the properties of operations. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models
4.NBT.B.6 Find whole-number quotients and remainders with up to four-digit dividends and one-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division.
NUMBER AND OPERATIONS: FRACTIONS
Extend understanding of fraction equivalence and ordering
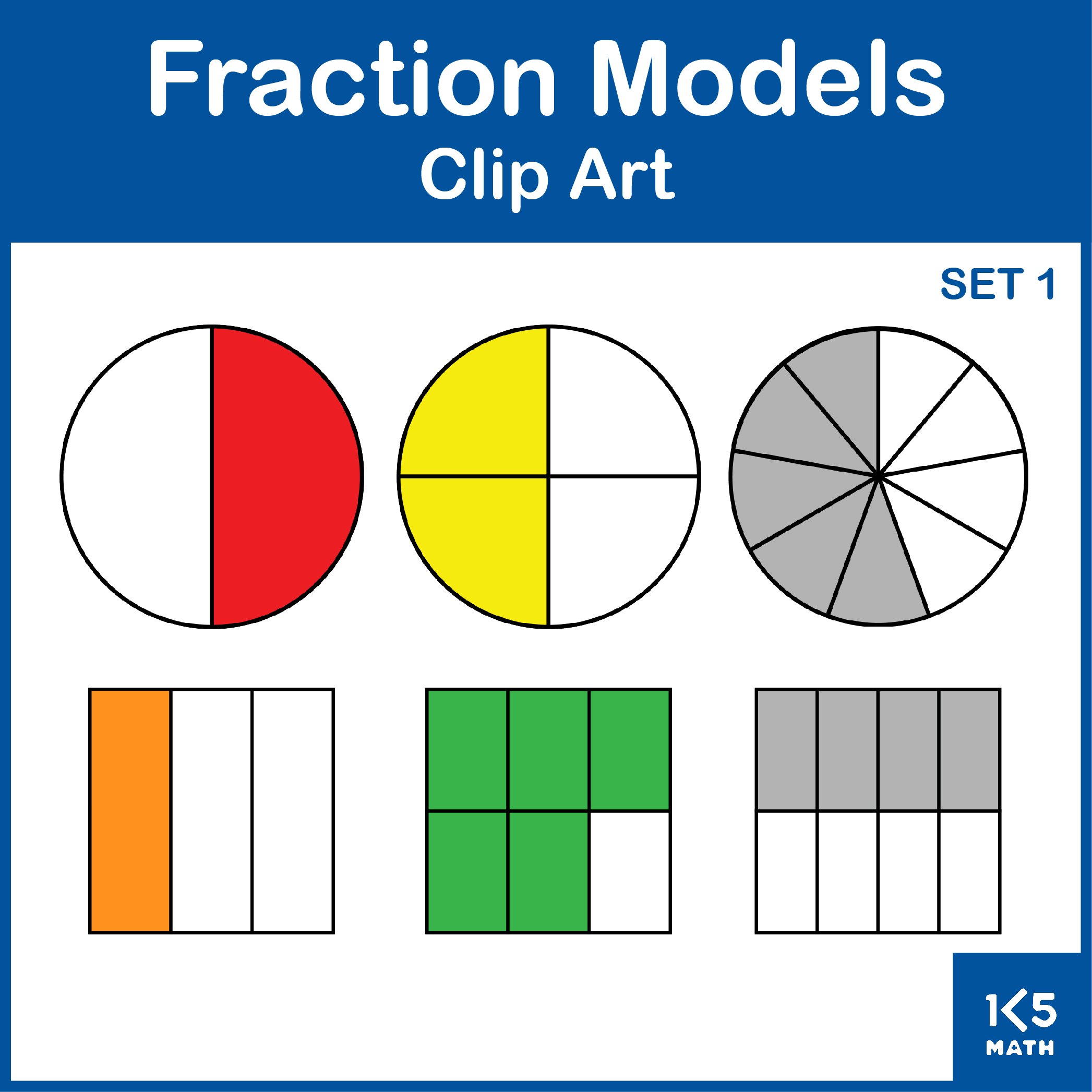
4.NF.A.1 Explain why a fraction a/b is equivalent to a fraction (nxa)/(nxb) by using visual fraction models, with attention to how the number and size of the parts differ even though the two fractions themselves are the same size. Use this principle to recognize and generate equivalent fractions.
4.NF.A.2 Compare two fractions with different numerators and different denominators, e.g. by creating common denominators or numerators, or by comparing to a benchmark fraction such as ½. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with comparisons with symbols >, =, or <. and justify the conclusions, e.g., by using a visual fraction model.
Build fractions from unit fractions by applying and extending previous understandings of operations on whole numbers
4.NF.B.3 Understand a fraction a/b with a>1 as a sum of fractions 1/b.
a. Understand addition and subtraction of fractions as joining and separating parts referring to the same whole.
b. Decompose a fraction into a sum of fraction with the same denominator in more than one way, recording each decomposition by an equation. Justify decompositions, e.g., by using a visual fraction model. Examples: 3/8 = 1/8 + 1/8 + 1/8; 3/8 = 1/8 + 2/8; 2 1/8 = 1 + 1 + 1/8 = 8/8 + 8/8 + 1/8
c. Add and subtract mixed numbers with like denominators, e.g., by replacing each mixed number with an equivalent fraction, and/or by using properties of operations and the relationship between addition and subtraction.
d. Solve word problems involving addition and subtraction of fractions referring to the same whole and having like denominators, e.g., by using visual fraction models and equations to represent the problem.
4.NF.B.4 Apply and extend previous understandings of multiplication to multiply a fraction by a whole number:
a. Understand a fraction a/b as a multiple of 1/b. For example, use a visual fraction model to represent 5/4 as the product of 5 x (1/4), recording the conclusion by the equation 5/4 = 5 x (1/4).
b. Understand a multiple of a/b as a multiple of 1/b, and use this understanding to multiply a fraction by a whole number. For example, use a visual fraction model to express 3 x (2/5) as 6 x (1/5), recognizing this product as 6/5. (In general, n x (a/b) =(nxa)/b)
c. Solve word problems involving multiplication of a fraction by a whole number, e.g. by using visual fraction models and equations to represent the problem. For example, if each person at a party will eat 3/8 of a pound of roast beef, and there will be 5 people at the party, how many pounds of roast beef will be needed? Between what two whole numbers does your answer lie?
Understand decimal notation for fractions, and compare decimal fractions
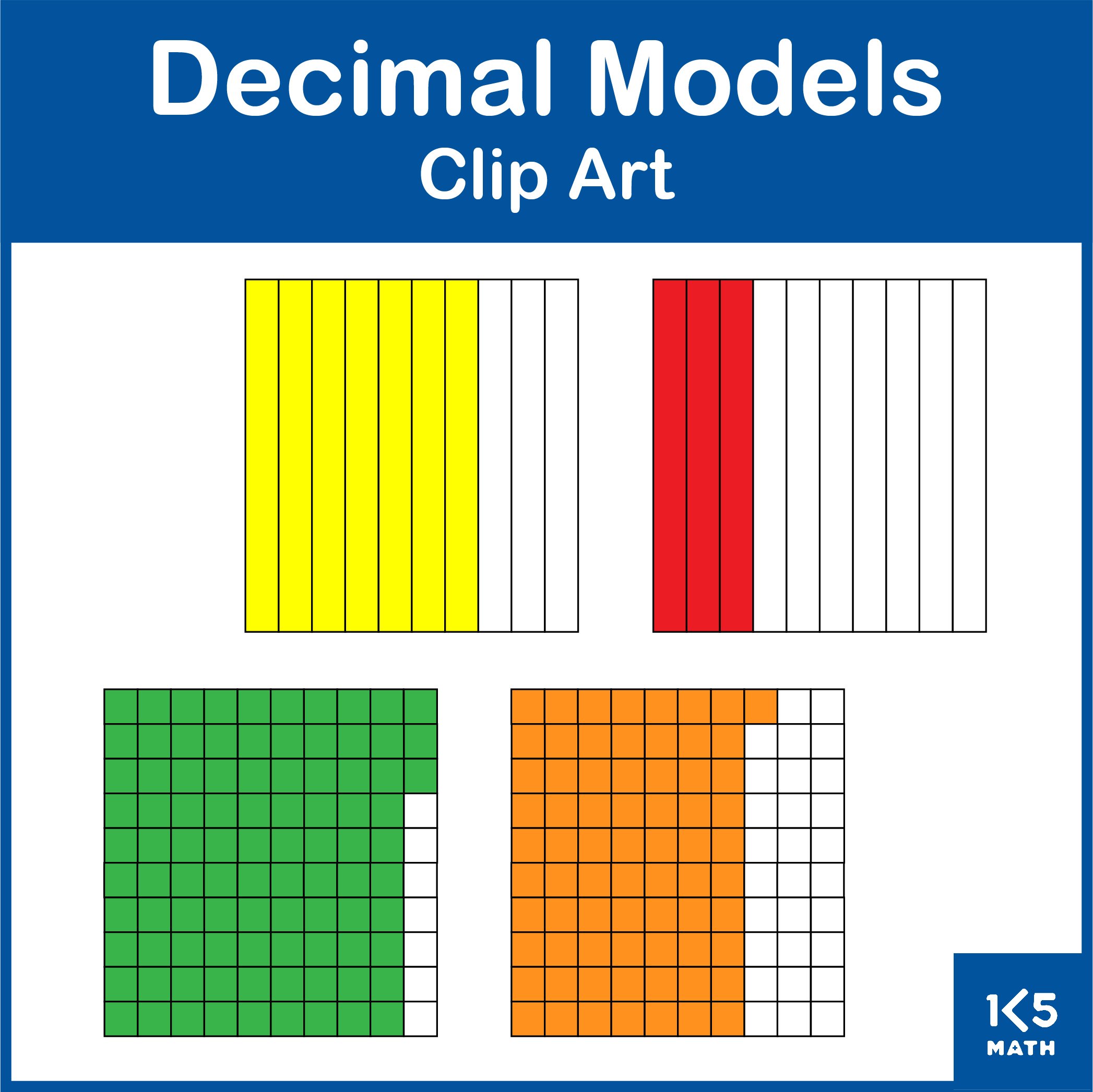
4.NF.C.5 Express a fraction with denominator 10 as an equivalent fraction with denominator 100, and use this technique to add two fractions with respective denominators 10 and 100. For example, express 3/10 as 30/100, and add 3/10 + 4/100 = 34/100.
4.NF.C.6 Use decimal notation for fractions with denominators 10 or 100. For example, rewrite 0.62 as 62/100; describe a length as 0.62 meters; locate 0.62 on a number line diagram.
4.NF.C.7 Compare two decimals to hundredths by reasoning about their size. Recognize that comparisons are valid only when the two decimals refer to the same whole. Record the results of comparisons with the symbols >, =, or <, and justify the conclusions, e.g., by using a visual model.