3RD GRADE NUMBER
This page provides sample downloads from some of the resources in 3rd Grade Mega Math Bundle aligned with the 3rd Grade Number Common Core State Standards. Try some of the samples listed in blue below each standard or download the bundle and have instant access to hundreds of easy-prep, engaging resources to simplify your math lesson planning and make active engagement through hands-on math instruction an integral part of your third grade classroom.
OPERATIONS AND ALGEBRAIC THINKING
Represent and solve problems involving multiplication and division
3.OA.A.1 Interpret products of whole numbers, e.g. interpret 5 x 7 as the total number of objects in 5 groups of 7 objects each. For example, describe a context in which a total number of objects can be expressed as 5 x 7.
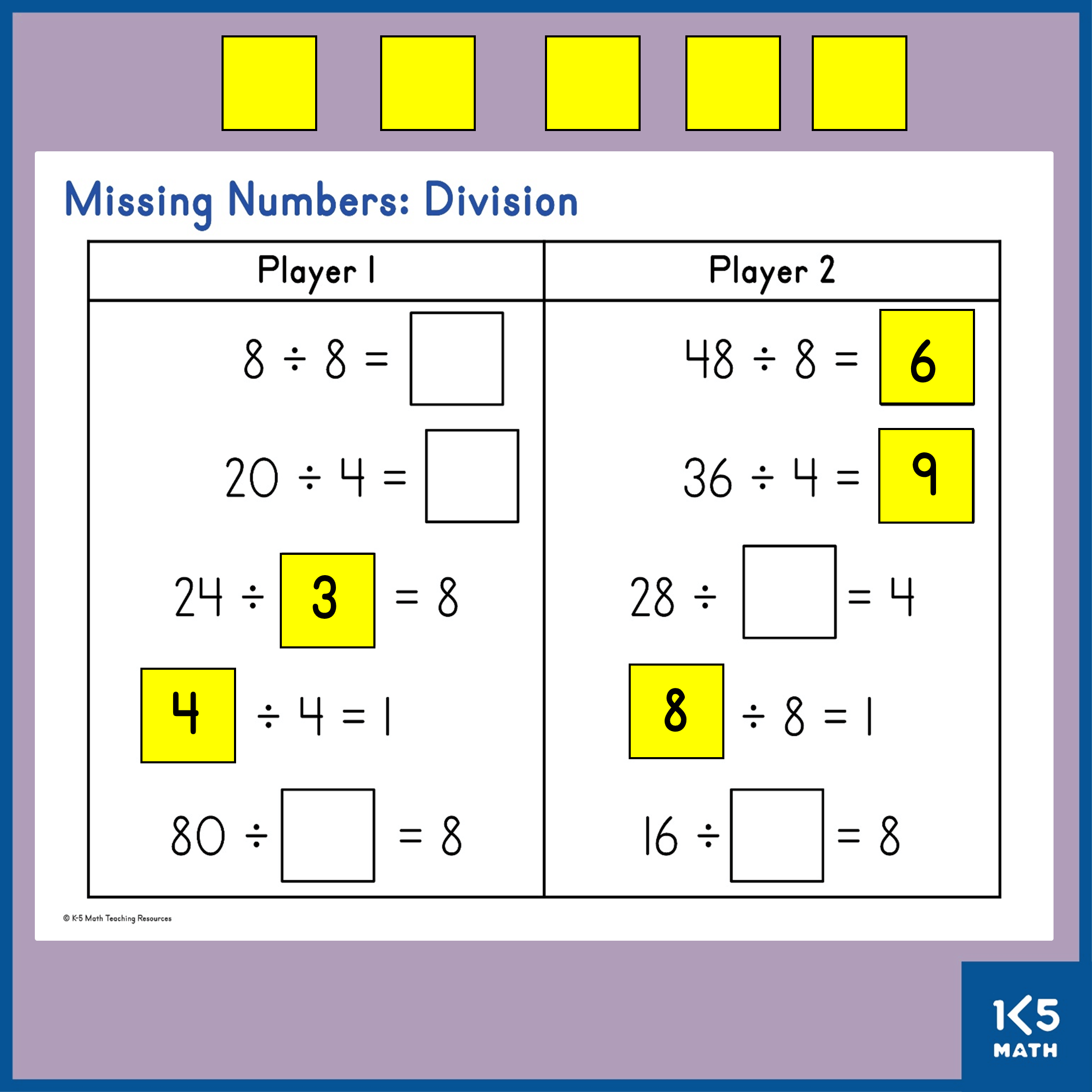
3.OA.A.2 Interpret whole-number quotients of whole numbers, e.g. interpret 56÷8 as the number of objects in each share when 56 objects are partitioned equally into 8 shares, or as a number of shares when 56 objects are partitioned into equal shares of 8 objects each. For example, describe a context in which a number of shares or a number of groups can be expressed as 56 ÷ 8.
3.OA.A.3 Use multiplication and division within 100 to solve word problems in situations involving equal groups, arrays, and measurement quantities, e.g. by using drawings and equations with a symbol for the unknown number to represent the problem.
Literature Links:
3.OA.A.4 Determine the unknown whole number in a multiplication or division equation relating three whole numbers. For example, determine the unknown number that makes the equation true in each of the equations 8 x?=48, 5 = ?÷3, 6x6 =?
Understand properties of multiplication and the relationship between multiplication and division
3.OA.B.5 Apply properties of operations as strategies to multiply and divide. Examples: If 6x4=24 is known then 4x6=24 is also known (Commutative property of multiplication.) 3x5x2 can be found by 3x5=15, then 15x2=30, or by 5x2=10, then 3x10=30 (Associative property of multiplication). Knowing that 8x5=40 and 8x2=16, one can find 8x7 as 8 x (5+2) = (8x5) + (8x2) = 40 +16 =56 (Distributive property).
3.OA.B.6 Understand division as an unknown-factor problem. For example, find 32 ÷ 8 by finding the number that makes 32 when multiplied by 8.
Multiply and divide within 100
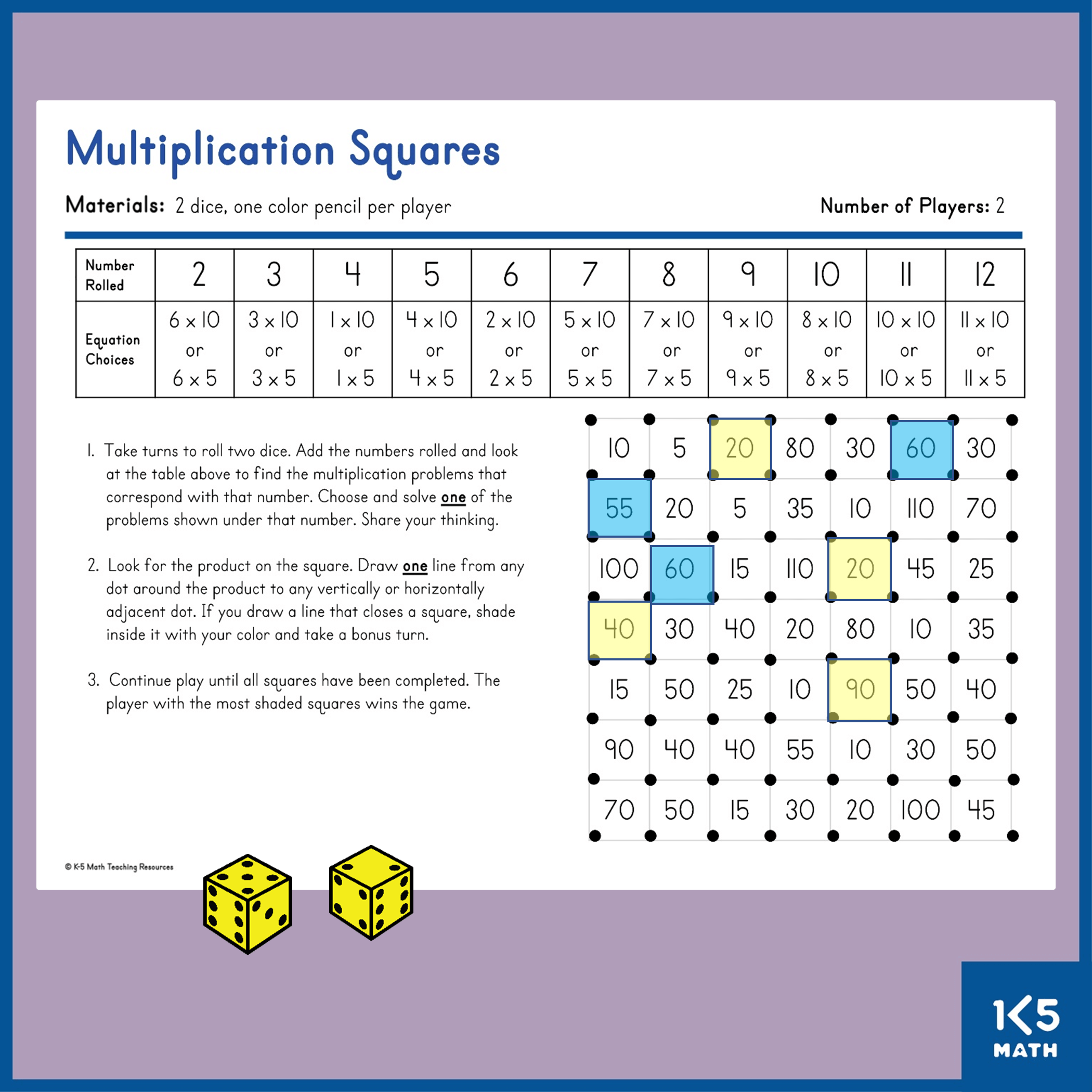
3.OA.C.7 Fluently multiply and divide within 100, using strategies such as the relationship between multiplication and division (e.g., knowing that 8x5=40, one knows 40÷5=8) or properties of operations. By the end of Grade 3, know from memory all products of two one-digit numbers.
Solve problems involving the four operations, and identify and explain patterns in arithmetic
3.OA.D.8 Solve two-step word problems using the four operations. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding.
3.OA.D.9 Identify arithmetic patterns (including patterns in the addition table or multiplication table), and explain them using properties of operations. For example, observe that 4 times a number is always even, and explain why 4 times a number can be decomposed into two equal addends.
NUMBER AND OPERATIONS IN BASE TEN
Use place value understanding and properties of operations to perform multi-digit arithmetic
3.NBT.A.1 Use place value understanding to round whole numbers to the nearest 10 or 100.
3.NBT.A.2 Fluently add and subtract within 1000 using strategies and algorithms based on place value, properties of operations, and/or the relationship between addition and subtraction.
3.NBT.A.3 Multiply one-digit whole numbers by multiples of 10 in the range 10-90 (e.g., 9x80, 5x60) using strategies based on place value and properties of operations.
NUMBER AND OPERATIONS: FRACTIONS
Develop understanding of fractions as numbers
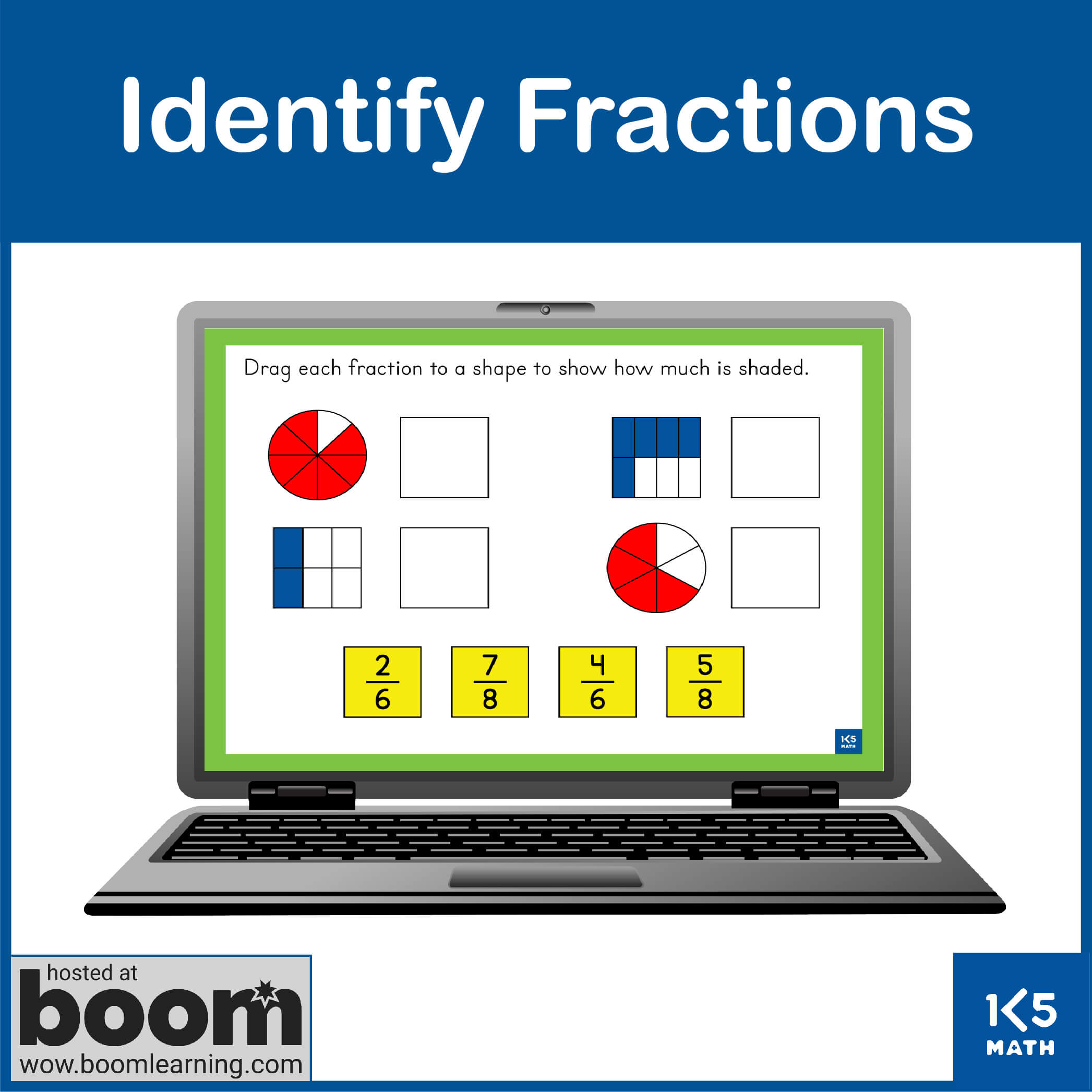
3.NF.A.1 Understand a fraction 1/b as a quantity formed by 1 part when a whole is partitioned into b equal parts: understand a fraction a/b as the quantity formed by a parts of size 1/b.
3.NF.A.2 Understand a fraction as a number on the number line; represent fractions on a number line diagram.
a. Represent a fraction 1/b on a number line diagram by defining the interval from 0 to 1 as the whole and portioning it into b equal parts. Recognize that each part has size 1/b and that the endpoint of the part based at 0 locates the number 1/b on the number line.
b. Represent a fraction a/b on a number line diagram by marking off a lengths 1/b from 0. Recognize that the resulting interval has size a/b and that its endpoint locates the number a/b on the number line.
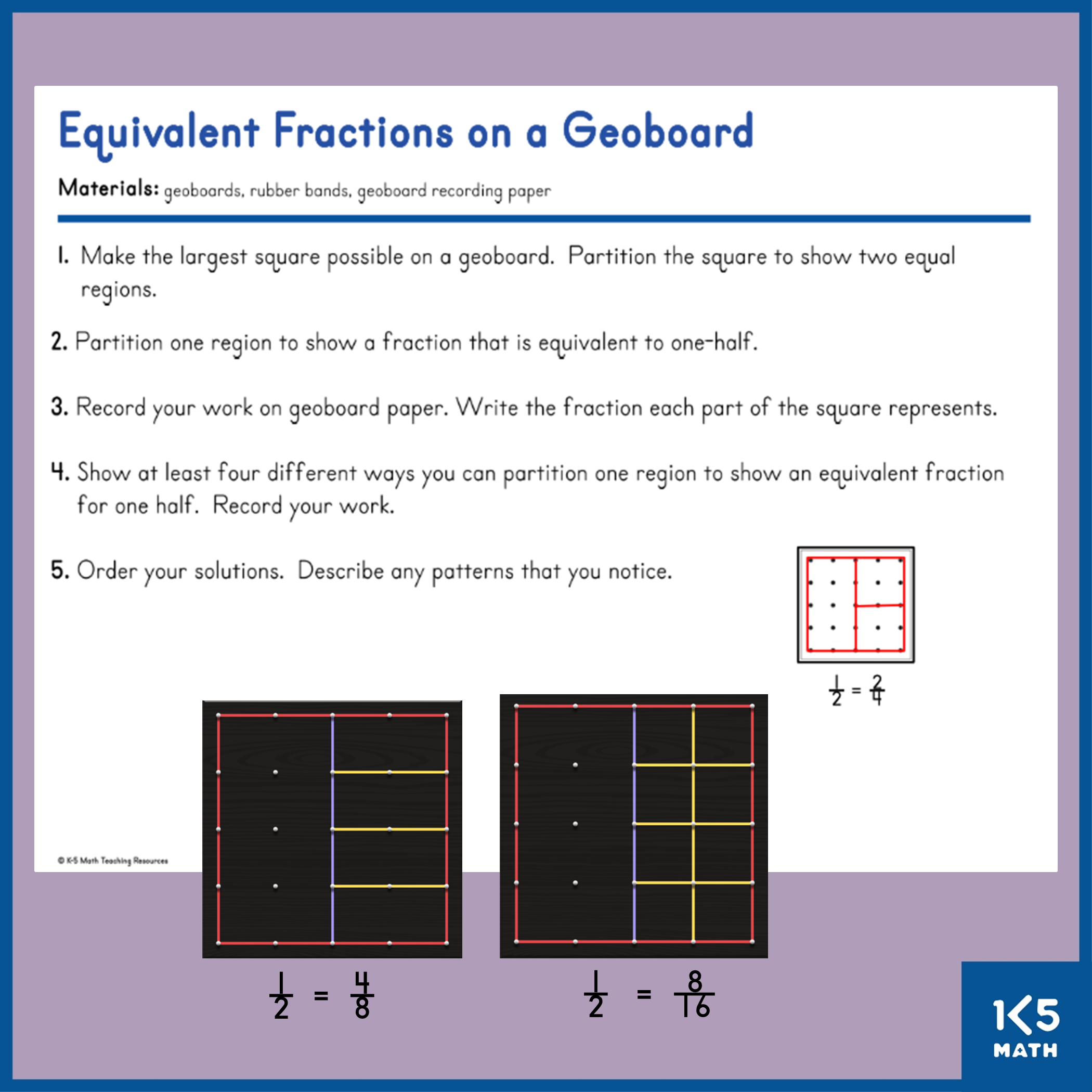
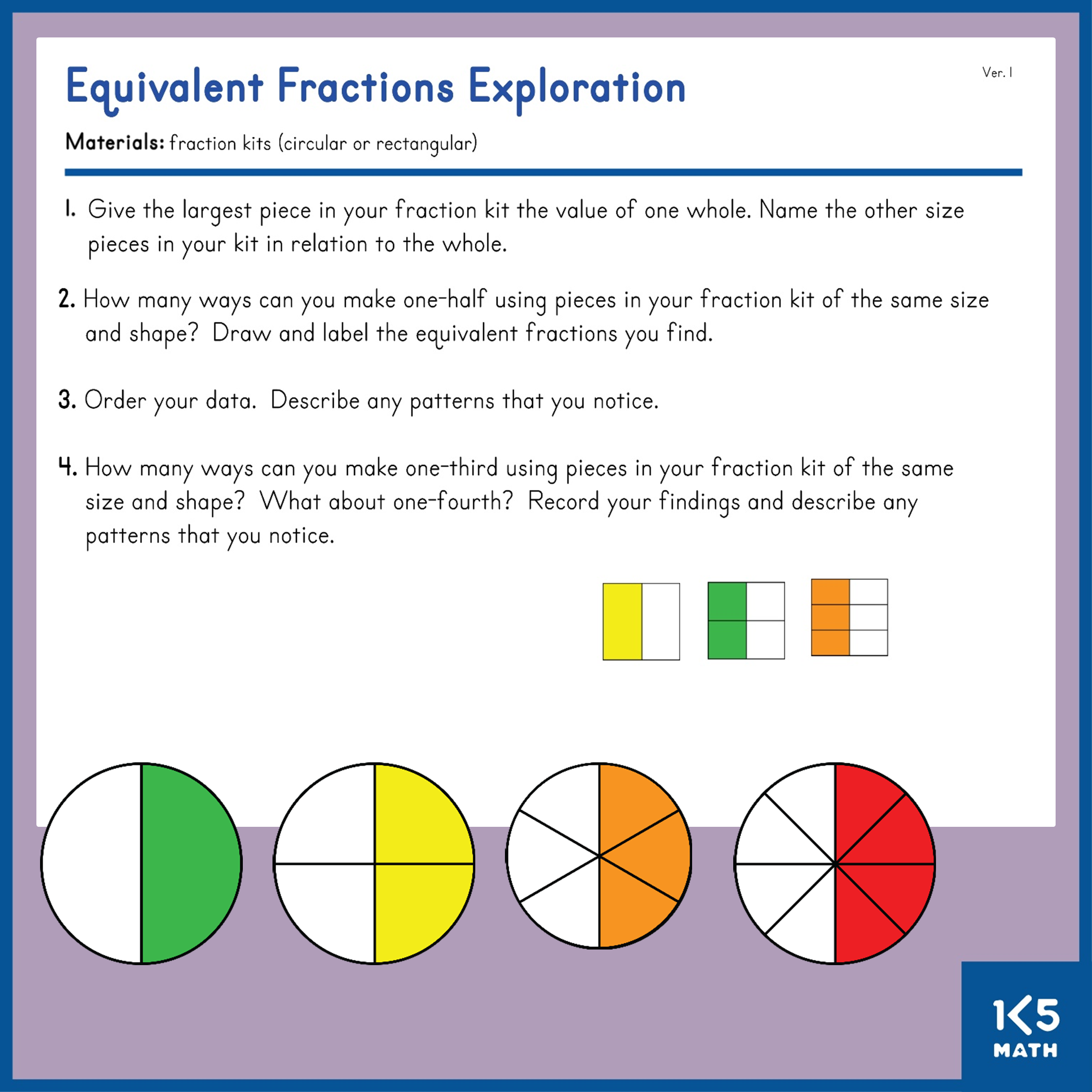
3.NF.A.3 Explain equivalence of fractions in special cases, and compare fractions by reasoning about their size.
a. Understand two fractions as equivalent (equal) if they are the same size, or the same point on a number line.
b. Recognize and generate simple equivalent fractions e.g., ½ = 2/4, 4/6 = 2/3. Explain why the fractions are equivalent, by using a visual model.
c. Express whole numbers as fractions, and recognize fractions that are equivalent to whole numbers. Examples: Express 3 in the form 3 = 3/1; recognize that 6/1 = 6; locate 4/4 and 1 at the same point of a number line diagram.
d. Compare two fractions with the same numerator or the same denominator by reasoning about their size. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with the symbols >, =, or < and justify the conclusions, e.g., by using a visual fraction model.